2022年春秋杯网络安全联赛春季赛·Crypto WP

2022年春秋杯网络安全联赛春季赛·Crypto

勇者山峰与传说殿堂都看了题

九点开始守着看的是勇者山峰

当时只有了一道300分的题

notKnapsack

题目

#!/usr/bin/python3
# -*- coding: utf-8 -*-
import random

from Crypto.Util.number import bytes_to_long
from secret import FLAG

assert FLAG.startswith(b'flag{') and FLAG.endswith(b'}')

q = 210767327475911131359308665806489575328083

flag_bin = bin(bytes_to_long(FLAG[5:-1]))[2:]
l = len(flag_bin)

n = random.randint(l, 2*l)
cipher = []
for _ in range(n):
    r = [random.randint(2, q-2) for _ in range(l)]
    s = 1
    for i in range(l):
        s = s * r[i] ** int(flag_bin[i]) % q
    cipher.append([r, s])

with open('output.txt', 'w') as f:
    f.write(str(cipher))

• output.txt

对output简单处理了下，然后分析加密代码，可知这是累积的特殊背包问题，搜寻无果，z3不好用。

仔细看题目，说不是背包，或许另有妙计。

时间已过去两个半小时。

十一点半，刷新发现又上了一道500分题

Train

题目

from Crypto.Util.number import*
from hashlib import sha256
import socketserver
import signal
import string
import random
from secret import flag

banner = br'''
 .oooooo..o                             oooo  oooo  ooooooooooooo                     o8o              
d8P'    `Y8                             `888  `888  8'   888   `8                     `"'              
Y88bo.      ooo. .oo.  .oo.    .oooo.    888   888       888      oooo d8b  .oooo.   oooo  ooo. .oo.   
 `"Y8888o.  `888P"Y88bP"Y88b  `P  )88b   888   888       888      `888""8P `P  )88b  `888  `888P"Y88b  
     `"Y88b  888   888   888   .oP"888   888   888       888       888      .oP"888   888   888   888  
oo     .d8P  888   888   888  d8(  888   888   888       888       888     d8(  888   888   888   888  
8""88888P'  o888o o888o o888o `Y888""8o o888o o888o     o888o     d888b    `Y888""8o o888o o888o o888o 
'''

n0 = 30798082519452208630254982405300548841337042015746308462162479889627080155514391987610153873334549377764946092629701
g = 64146569863628228208271069055817252751116365290967978172021890038925428672043

def TrainHash(msg):
    n = n0
    msg = map(ord,msg)
    for i in msg :
        n = g * (n+i)
        n = n & (1<<383)
    return n - 0xf5e33dabb114514

table = string.ascii_letters+string.digits

MENU = br'''
<OPTION>
'''

class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self, prompt=b'SERVER <INPUT>: '):
        self.send(prompt, newline=False)
        return self._recvall()

    def proof_of_work(self):
        proof = (''.join([random.choice(table)for _ in range(20)])).encode()
        sha = sha256(proof).hexdigest().encode()
        self.send(b"[+] sha256(XXXX+" + proof[4:] + b") == " + sha )
        XXXX = self.recv(prompt = b'[+] Plz Tell Me XXXX :')
        if len(XXXX) != 4 or sha256(XXXX + proof[4:]).hexdigest().encode() != sha:
            return False
        return sha.decode()

    def handle(self):
        signal.alarm(30)
        FirstBlockHash = self.proof_of_work()
        if not FirstBlockHash:
            self.request.close()
        self.send(banner)
        self.send(b"\nPlease give me 2 strings that are same when are hashed  =.=  ")
        string1 = self.recv().decode()
        string2 = self.recv().decode()

        if TrainHash(string1) == TrainHash(string2):
            self.send(b'\nJust do it!~ You can do more!')
            if string2.encode()[-50:] == string1.encode()[-50:]:
                self.send(flag)
        self.send(b"\nConnection has been closed  =.=  ")
        self.request.close()

class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass

class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass

if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 10012
    print("HOST:POST " + HOST+":" + str(PORT))
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

简单审计代码，不了解的hash方式。

无所谓，朴素地想着先写py脚本连上靶机互动一下

结果，发了两个字符串flag，直接送给我了flag🤔

回去看代码，发现确实没限定string长度，不好的题目

import socket
import sys

HOST = '写自己的HOST'  # str
PORT = 自己的端口  # int

s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
s.connect((HOST, PORT))
a = str(s.recv(1024))
print(a)
print(s.recv(1024))
data = ''.join(a.strip("\n"))
sha_key = ''.join(data.split(')')[0]).split('+')[-1]  # like: dygRhRVGRA146H43
print(sha_key)
sha_data = data.split('== ')[-1][:-3]  # like: d06a5396ad875acdf0796cc5b0c083170e38728847085cfd99dadaeda71a3d17
print(sha_data)
import hashlib


# 第一关 sha256
def decry(data):
    s = hashlib.sha256()  # Get the hash algorithm.
    s.update(data.encode())  # Hash the data.
    b = s.hexdigest()  # Get he hash value.
    return b


list1 = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J",
         "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z", "a", "b", "c", "d", "e", "f",
         "g", "h", "i", "j", "k", "l", "m", "n", "o",
         "p", "q", "r", "s", "t", "u", "v", "w", "x", "y", "z", 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ]


def yi():
    for a in list1:
        for b in list1:
            for c in list1:
                for d in list1:
                    flag = "{0}{1}{2}{3}{4}".format(a, b, c, d, sha_key)
                    flag_sha = decry(flag)
                    flag1 = flag[0:4]

                    if str(flag_sha) == str(sha_data):
                        print('恭喜！')
                        return str(flag1)


s.send((yi()+'\n').encode())
print(s.recv(1024))
print(s.recv(1024))
s.send('flag\n'.encode())
s.send('flag\n'.encode())
print(s.recv(1024))
print(s.recv(1024))
print(s.recv(1024))
print(s.recv(1024))

做核酸、洗澡、睡觉等事件干扰，下午三点左右方才又来看题。

想着勇者山峰没什么了，就登陆了传说殿堂

🤔奇妙啊，一样的题，一样的打法

发现绝对厉害的都在传说殿堂，相对厉害的全在勇者山峰

（到比赛结束前，传说殿堂出一道密码就已经是前30了，勇者前90

然后就去看了

TrainPlus

from MD_Train import MD00Plus
from hashlib import sha256
import socketserver
import signal
import string
import random
import os
from secret import flag


banner = br'''
ooooooooooooo                     o8o              ooooooooo.   oooo
8'   888   `8                     `"'              `888   `Y88. `888
     888      oooo d8b  .oooo.   oooo  ooo. .oo.    888   .d88'  888  oooo  oooo   .oooo.o
     888      `888""8P `P  )88b  `888  `888P"Y88b   888ooo88P'   888  `888  `888  d88(  "8
     888       888      .oP"888   888   888   888   888          888   888   888  `"Y88b.
     888       888     d8(  888   888   888   888   888          888   888   888  o.  )88b
    o888o     d888b    `Y888""8o o888o o888o o888o o888o        o888o  `V88V"V8P' 8""888P'
'''
table = string.ascii_letters+string.digits
sec = os.urandom(random.randrange(1,26))
GreatThing = os.urandom(16)

class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self, prompt=b'SERVER <INPUT>: '):
        self.send(prompt, newline=False)
        return self._recvall()

    def proof_of_work(self):
        proof = (''.join([random.choice(table)for _ in range(20)])).encode()
        sha = sha256(proof).hexdigest().encode()
        self.send(b"[+] sha256(XXXX+" + proof[4:] + b") == " + sha )
        XXXX = self.recv(prompt = b'[+] Plz Tell Me XXXX :')
        if len(XXXX) != 4 or sha256(XXXX + proof[4:]).hexdigest().encode() != sha:
            return False
        return sha.decode()

    def handle(self):
        signal.alarm(30)
        FirstBlockHash = self.proof_of_work()
        if not FirstBlockHash:
            self.request.close()


        self.send(banner)
        self.send(b":) My Great Thing:" + GreatThing )
        self.send(b":) The MD00Plus of my GREATTHING:" + MD00Plus(sec).encode())

        for i in range(25):
            self.send(b"Please tell me the msg ")
            msg = self.recv()
            self.send(b"Please tell me the hash you can forcast.")
            msg,Hash = msg.split(b',')
            msg = bytes.fromhex(msg.decode())
            Hash = bytes.fromhex(Hash.decode())
            if GreatThing not in msg:
                self.send(b"[!]INVALID!")
                continue
            elif MD00Plus(sec + msg).encode() == Hash:
                self.send(flag)
                break
            else:
                self.send(b'You Wrong!')

        self.request.close()

class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass

class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass

if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 10114
    print("HOST:POST " + HOST+":" + str(PORT))
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

def MD00Plus(message: bytes):
    h0 = 0x114514ab
    h1 = 0x1919810a
    h2 = 0xa0189191
    h3 = 0xba415411

    R = (7, 12, 17, 22) * 4 + (5, 9, 14, 20) * 4 + (4, 11, 16, 23) * 4 + (6, 10, 15, 21) * 4
    K = (0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee,
         0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501, 0x698098d8,
         0x8b44f7af, 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193,
         0xa679438e, 0x49b40821, 0xf61e2562, 0xc040b340, 0x265e5a51,
         0xe9b6c7aa, 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8,
         0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905,
         0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a, 0xfffa3942, 0x8771f681,
         0x6d9d6122, 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60,
         0xbebfbc70, 0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05,
         0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665, 0xf4292244,
         0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92,
         0xffeff47d, 0x85845dd1, 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314,
         0x4e0811a1, 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391)

    F = lambda x, y, z: ((x & y) | ((~x) & z))
    G = lambda x, y, z: ((x & z) | (y & (~z)))
    H = lambda x, y, z: (x ^ y ^ z)
    I = lambda x, y, z: (y ^ (x | (~z)))

    L = lambda x, n: ((x << n) | (x >> (32 - n))) & 0xffffffff
    W = lambda i4, i3, i2, i1: (i1 << 24) | (i2 << 16) | (i3 << 8) | i4
    reverse = lambda x: (x << 24) & 0xff000000 | (x << 8) & 0x00ff0000 | \
                        (x >> 8) & 0x0000ff00 | (x >> 24) & 0x000000ff

    ascii_list = list(map(lambda x: x, message))
    msg_length = len(ascii_list) * 8
    ascii_list.append(128)

    while (len(ascii_list) * 8 + 64) % 512 != 0:
        ascii_list.append(1)

    for i in range(8):
        ascii_list.append((msg_length >> (8 * i)) & 0xff)

    for i in range(len(ascii_list) // 64):
        a, b, c, d = h0, h1, h2, h3
        for j in range(64):
            if 0 <= j <= 15:
                f = F(b, c, d) & 0xffffffff
                g = j
            elif 16 <= j <= 31:
                f = G(b, c, d) & 0xffffffff
                g = ((5 * j) + 1) % 16
            elif 32 <= j <= 47:
                f = H(b, c, d) & 0xffffffff
                g = ((3 * j) + 5) % 16
            else:
                f = I(b, c, d) & 0xffffffff
                g = (7 * j) % 16
            aa, dd, cc = d, c, b
            s = i * 64 + g * 4
            w = W(ascii_list[s], ascii_list[s + 1], ascii_list[s + 2], ascii_list[s + 3])
            bb = (L((a + f + K[j] + w) & 0xffffffff, R[j]) + b) & 0xffffffff
            a, b, c, d = aa, bb, cc, dd
        h0 = (h0 + a) & 0xffffffff
        h1 = (h1 + b) & 0xffffffff
        h2 = (h2 + c) & 0xffffffff
        h3 = (h3 + d) & 0xffffffff
    h0, h1, h2, h3 = reverse(h0), reverse(h1), reverse(h2), reverse(h3)
    digest = (h0 << 96) | (h1 << 64) | (h2 << 32) | h3
    return hex(digest)[2:].rjust(32, '0')

明显感觉到复杂，没什么人出加上自己调试了半天，交互不好，作罢

看回了传说殿堂第一题

bob’s enc

from secret import *
import random

prime =  2141
print len(flag)
flag = map(ord,flag)
flag1 = flag[:21]
flag2 = flag[21:]
row = 64

def add(msg1,msg2):
    return [(x+y)%prime for x,y in zip(msg1,msg2)]

def multi(msg1,msg2):
    out = []
    for l in msg1:
        s = 0
        for x,y in zip(l,msg2):
            s += (x*y)%prime
            s %= prime
        out.append(s)
    return out
def genkey(leng):
    l = [[] for i in range(row)]
    for x in range(row):
        for i in range(leng):
            l[x].append(random.randint(0,511))
    return l

key = genkey(len(flag1))
print key

cipher1 = multi(key,flag1)

print cipher1

cipher2 = multi(key,flag2)

noise = [random.randint(0,6) for i in range(row)]
print add(noise,cipher2)

[[185, 96, 351, 118, 421, 449, 350, 349, 388, 95, 341, 327, 29, 156, 399, 283, 292, 461, 445, 120, 126], [495, 358, 192, 300, 279, 277, 478, 335, 231, 241, 178, 314, 453, 251, 133, 391, 213, 132, 254, 388, 46], [428, 44, 100, 483, 12, 311, 57, 443, 289, 90, 478, 495, 399, 89, 324, 275, 322, 99, 343, 489, 133], [420, 358, 472, 260, 267, 136, 303, 491, 390, 248, 430, 117, 154, 244, 62, 217, 204, 334, 277, 231, 325], [11, 96, 61, 67, 456, 361, 292, 278, 424, 237, 345, 109, 475, 473, 29, 250, 195, 430, 114, 13, 199], [17, 91, 330, 73, 384, 134, 437, 161, 166, 185, 499, 491, 342, 129, 348, 162, 478, 216, 189, 311, 502], [396, 437, 98, 421, 120, 443, 113, 432, 9, 476, 243, 122, 416, 508, 287, 45, 84, 322, 504, 287, 251], [187, 489, 407, 204, 127, 10, 302, 101, 389, 113, 469, 184, 249, 131, 113, 18, 350, 106, 486, 406, 295], [265, 425, 30, 478, 471, 211, 162, 323, 163, 205, 187, 422, 452, 226, 230, 367, 478, 229, 365, 395, 294], [360, 193, 180, 253, 337, 453, 16, 352, 243, 107, 171, 46, 25, 234, 46, 479, 267, 267, 171, 188, 127], [379, 360, 109, 360, 403, 343, 75, 306, 138, 40, 41, 253, 428, 401, 464, 495, 21, 296, 319, 410, 440], [28, 209, 1, 233, 458, 266, 301, 359, 469, 304, 264, 368, 339, 25, 490, 343, 404, 488, 275, 262, 274], [180, 372, 133, 341, 29, 352, 326, 89, 323, 479, 68, 76, 247, 225, 159, 163, 180, 160, 171, 7, 322], [322, 295, 28, 467, 361, 169, 190, 71, 456, 140, 456, 202, 295, 424, 428, 18, 286, 233, 470, 303, 429], [234, 37, 128, 175, 282, 509, 54, 186, 177, 23, 348, 487, 473, 377, 81, 225, 154, 511, 364, 120, 280], [262, 82, 383, 490, 128, 448, 289, 420, 239, 374, 392, 149, 217, 398, 441, 480, 453, 503, 318, 285, 418], [0, 347, 223, 381, 469, 208, 424, 435, 404, 64, 107, 73, 490, 116, 445, 392, 194, 287, 66, 325, 261], [99, 26, 489, 114, 3, 351, 494, 174, 369, 354, 379, 187, 90, 202, 286, 37, 48, 397, 298, 65, 499], [455, 114, 349, 401, 5, 139, 314, 227, 134, 258, 270, 135, 287, 332, 298, 272, 167, 43, 271, 484, 177], [448, 78, 479, 324, 170, 7, 230, 173, 214, 65, 91, 497, 68, 391, 44, 205, 364, 471, 460, 312, 122], [452, 360, 448, 169, 240, 496, 302, 3, 354, 266, 46, 22, 151, 498, 461, 314, 169, 88, 30, 487, 258], [282, 222, 260, 503, 106, 420, 315, 307, 202, 238, 224, 329, 351, 190, 137, 294, 171, 309, 19, 186, 391], [69, 501, 283, 96, 159, 459, 437, 192, 293, 479, 79, 49, 299, 205, 177, 360, 36, 414, 118, 194, 270], [6, 419, 459, 254, 97, 455, 445, 239, 277, 278, 226, 23, 146, 151, 273, 378, 141, 281, 480, 388, 213], [181, 508, 347, 447, 467, 351, 503, 262, 375, 74, 49, 48, 364, 492, 400, 305, 25, 207, 278, 163, 11], [320, 94, 400, 15, 201, 53, 130, 137, 219, 57, 20, 239, 467, 352, 373, 395, 58, 4, 446, 332, 41], [205, 385, 446, 185, 470, 268, 308, 461, 265, 75, 75, 104, 108, 14, 334, 499, 207, 363, 94, 505, 363], [299, 292, 112, 203, 7, 240, 499, 343, 396, 482, 383, 61, 476, 101, 187, 265, 428, 53, 24, 342, 201], [421, 286, 305, 79, 324, 216, 163, 193, 362, 57, 472, 449, 169, 33, 280, 202, 237, 376, 382, 2, 1], [379, 33, 151, 51, 353, 295, 145, 220, 147, 251, 90, 344, 96, 31, 185, 250, 270, 420, 365, 373, 356], [228, 299, 87, 113, 458, 52, 26, 228, 294, 97, 384, 493, 380, 209, 257, 20, 375, 2, 316, 129, 492], [479, 346, 57, 488, 183, 185, 18, 422, 209, 318, 461, 159, 469, 145, 44, 58, 441, 490, 510, 194, 192], [254, 398, 510, 159, 371, 280, 331, 23, 99, 150, 175, 151, 42, 473, 164, 35, 97, 174, 115, 24, 270], [280, 76, 254, 293, 491, 76, 128, 301, 240, 357, 192, 372, 343, 34, 386, 468, 313, 41, 285, 507, 282], [271, 91, 507, 16, 128, 8, 326, 102, 355, 371, 313, 292, 433, 2, 459, 14, 258, 498, 146, 446, 309], [386, 88, 502, 4, 399, 272, 49, 69, 51, 465, 291, 289, 417, 271, 374, 337, 46, 393, 19, 429, 91], [407, 35, 337, 51, 41, 460, 222, 448, 499, 381, 59, 468, 440, 216, 86, 236, 91, 18, 123, 68, 145], [384, 30, 454, 419, 275, 164, 72, 195, 489, 458, 419, 148, 269, 150, 358, 188, 109, 27, 42, 34, 123], [500, 184, 195, 193, 68, 19, 329, 511, 280, 69, 113, 124, 102, 274, 43, 374, 408, 64, 314, 309, 473], [72, 145, 242, 2, 367, 371, 143, 166, 325, 74, 414, 94, 269, 196, 124, 94, 14, 351, 111, 465, 503], [70, 47, 439, 170, 306, 82, 233, 36, 346, 234, 157, 468, 83, 85, 424, 157, 258, 120, 270, 136, 286], [442, 173, 254, 271, 420, 507, 297, 473, 296, 511, 98, 133, 37, 498, 468, 17, 260, 318, 168, 490, 124], [50, 35, 252, 472, 406, 400, 439, 89, 309, 393, 332, 324, 260, 215, 8, 322, 357, 252, 124, 358, 457], [93, 102, 478, 224, 428, 10, 238, 368, 113, 502, 148, 7, 395, 97, 73, 306, 40, 395, 9, 254, 319], [282, 277, 295, 425, 59, 21, 136, 230, 207, 1, 29, 170, 14, 337, 371, 437, 359, 10, 100, 374, 24], [3, 270, 289, 179, 434, 489, 470, 343, 478, 156, 177, 72, 13, 266, 475, 23, 148, 102, 210, 270, 323], [464, 466, 277, 191, 426, 20, 266, 33, 41, 249, 452, 475, 265, 421, 282, 250, 233, 287, 495, 170, 300], [379, 35, 137, 106, 155, 81, 154, 382, 30, 237, 294, 478, 321, 384, 48, 111, 150, 4, 454, 446, 28], [57, 355, 94, 253, 297, 424, 415, 480, 68, 356, 415, 73, 41, 171, 491, 130, 92, 180, 506, 326, 463], [279, 43, 202, 35, 397, 257, 120, 11, 231, 369, 221, 332, 47, 236, 58, 278, 75, 117, 33, 130, 358], [142, 335, 339, 112, 38, 82, 426, 211, 174, 389, 137, 96, 431, 113, 112, 500, 145, 44, 313, 96, 187], [246, 211, 400, 415, 294, 234, 367, 46, 371, 479, 412, 197, 204, 498, 18, 140, 67, 237, 510, 457, 298], [258, 3, 136, 284, 149, 161, 456, 122, 114, 383, 251, 240, 453, 227, 330, 33, 241, 160, 306, 254, 409], [391, 115, 92, 102, 359, 182, 489, 313, 204, 275, 206, 447, 436, 286, 229, 377, 374, 162, 22, 384, 40], [427, 491, 362, 240, 358, 296, 154, 178, 278, 284, 324, 422, 52, 295, 490, 56, 39, 378, 174, 202, 496], [29, 454, 436, 6, 287, 82, 154, 474, 92, 272, 400, 238, 352, 140, 386, 504, 19, 32, 334, 30, 450], [469, 123, 353, 422, 175, 260, 294, 18, 268, 479, 60, 114, 456, 55, 403, 446, 166, 259, 294, 215, 48], [404, 187, 426, 362, 296, 239, 226, 416, 306, 336, 1, 448, 47, 403, 367, 357, 501, 425, 310, 41, 303], [339, 115, 478, 416, 10, 90, 188, 229, 217, 441, 288, 152, 394, 219, 422, 376, 325, 375, 6, 454, 238], [226, 226, 149, 107, 418, 419, 209, 108, 87, 127, 202, 320, 179, 234, 87, 335, 195, 5, 273, 142, 115], [464, 177, 77, 101, 76, 19, 73, 397, 296, 34, 360, 107, 491, 460, 510, 342, 198, 118, 105, 337, 239], [464, 25, 191, 113, 455, 129, 247, 488, 303, 27, 242, 423, 336, 125, 283, 332, 244, 372, 175, 276, 49], [211, 367, 406, 314, 177, 496, 320, 385, 193, 51, 423, 80, 258, 44, 154, 362, 215, 296, 260, 424, 160], [384, 161, 92, 402, 414, 443, 129, 279, 272, 224, 294, 319, 75, 169, 242, 85, 315, 402, 4, 268, 88]]
[1702, 795, 740, 373, 535, 1308, 1050, 502, 40, 672, 1354, 1843, 515, 231, 774, 65, 978, 1340, 455, 2137, 733, 307, 1604, 723, 1023, 1253, 275, 1817, 404, 2035, 267, 1475, 14, 2127, 15, 487, 317, 757, 290, 541, 100, 951, 2049, 1042, 1404, 1676, 655, 1460, 1532, 273, 916, 1454, 1690, 1628, 1751, 1656, 139, 156, 2102, 264, 243, 455, 1564, 2072]
[884, 1584, 681, 1713, 1916, 609, 1840, 177, 1723, 1049, 254, 864, 1671, 121, 2021, 1353, 1290, 1891, 556, 1786, 1553, 1548, 727, 1967, 1800, 422, 1559, 1290, 642, 1406, 441, 1928, 395, 279, 1125, 1273, 99, 1131, 395, 76, 733, 416, 924, 571, 506, 822, 877, 887, 860, 1755, 1385, 1861, 1754, 1851, 1046, 1724, 1866, 1427, 378, 351, 146, 1367, 756, 505]

la佬一🩸，好奇心拉满，于是开始研究起来了

化简，易得解flag1要点：单模多元线性同余方程

就着csdn现学，效率过低🤔

放弃之际，在github上搜到了优秀的代码

处理好数据，解方程，得到前半段flag

#!/usr/bin/python2
# -*- coding: utf-8 -*-

'''
Author @55-AA
19 July, 2016
'''

import copy


def gcd(a, b):
    """
    Return the greatest common denominator of integers a and b.
    gmpy2.gcd(a, b)
    """
    while b:
        a, b = b, a % b
    return a


def lcm(a, b):
    return a * b / (gcd(a, b))


def egcd(a, b):
    """
    ax + by = 1
    ax ≡ 1 mod b
    Return a 3-element tuple (g, x, y), the g  = gcd(a, b)
    gmpy2.gcdext(a, b)
    """
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)


def mod_inv(a, m):
    """
    ax ≡ 1 mod m
    gmpy2.invert(a, m)
    """
    g, x, y = egcd(a, m)
    assert g == 1
    return x % m


def int2mem(x):
    """
    0x12233 => '\x33\x22\x01'
    """
    pad_even = lambda x: ('', '0')[len(x) % 2] + x
    x = list(pad_even(format(x, 'x')).decode('hex'))
    x.reverse()
    return ''.join(x)


def mem2int(x):
    """
    '\x33\x22\x01' => 0x12233
    """
    x = list(x)
    x.reverse()
    return int(''.join(x).encode('hex'), 16)


###########################################################
# class
###########################################################
class GaussMatrix:
    """
    A*X ≡ B (mod p),p为大于0的整数。

    高斯消元求解模线性方程组。先化简为上三角，然后回代求解。
    当r(A) <= n时，一定有多解；
    当r(A) == n时，有多解或唯一解；
    当r(A) != r(A~)时，无解。
    r(A)为系数矩阵的秩，r(A)为增广矩阵的秩，n为未知数的个数。

    http://www.docin.com/p-1063811671.html讨论了gcd(|A|, m) = 1时的LU分解解法，
    本文包括了gcd(|A|, m) > 1时的解法，

    化简原则：
        1、系数与模互质
        2、系数加某一行n次后，对应的系数与模的GCD最小
        3、将1或2得到的系数移到对角线上

    初始化参数：
        matrix：方程组的增广矩阵（最后一列为常数项）。
            matrix = [
                [ 69,  75,  78,  36,  58],
                [ 46,  68,  51,  26,  42],
                [ 76,  40,  42,  49,  11],
                [ 11,  45,   2,  45,   1],
                [ 15,  67,  60,  14,  72],
                [ 76,  67,  73,  56,  58],
                [ 67,  15,  68,  54,  75],
            ]    
        mod：模数

    函数：
        gauss()：求解方程

    输出变量：
        error_str：出错的信息
        count：解的数量
    """

    def __init__(self, matrix, mod):
        self.matrix = copy.deepcopy(matrix)
        self.d = None

        self.r = len(matrix)
        self.c = len(matrix[0])
        self.N = len(matrix[0]) - 1
        self.mod = mod
        self.count = 1
        self.error_str = "unknown error"

    def verify_solution(self, solution):
        for d in self.matrix:
            result = 0
            for r in map(lambda x, y: 0 if None == y else x * y, d, solution):
                result += r
            if (result % self.mod) != ((d[-1]) % self.mod):
                return 0
        return 1

    def swap_row(self, ra, rb):
        (self.d[ra], self.d[rb]) = (self.d[rb], self.d[ra])

    def swap_col(self, ca, cb):
        for j in range(self.r):
            (self.d[j][ca], self.d[j][cb]) = (self.d[j][cb], self.d[j][ca])

    def inv_result(self, r, n):
        """
        求解第n个未知数，r已经获得的解。形如：[None,None, ..., n+1, ...]

        a*x ≡ b(mod m)
        x有解的条件：gcd(a,m) | b。也即a,m互质时一定有解，不互质时，b整除gcd(a,m)也有解，否则无解。
        解的格式为：x0+k(m/gcd(a,m))，其中x0为最小整数特解，k为任意整数。
        返回[x0, x1, ...xn]，其中x0 < x1 < xn < m。
        """
        b = self.d[n][self.N]
        a = self.d[n][n]
        m = self.mod
        k = gcd(a, m)
        for j in xrange(n + 1, self.N):
            b = (b - (self.d[n][j] * r[j] % m)) % m

        if 1 == k:
            return [mod_inv(a, m) * b % m]
        else:
            if k == gcd(k, b):
                a /= k
                b /= k
                m /= k

                x0 = mod_inv(a, m) * b % m
                x = []
                for i in xrange(k):
                    x.append(x0 + m * i)
                return x
        return None

    def find_min_gcd_row_col(self, i, j):
        # 查找直接互质的对角线系数
        for k in xrange(i, self.r):
            for l in xrange(j, self.c - 1):
                if (1 == gcd(self.d[k][l], self.mod)):
                    return [k, l]

        def add_min_gcd(a, b, m):
            r = [m, 1]
            g = gcd(a, b)
            if g:
                i = a / g
                for j in xrange(i):
                    g = gcd((a + j * b) % m, m)
                    if g < r[0]:
                        r[0] = g
                        r[1] = j
                    if g == 1:
                        break
            return r

        # 查找加乘后GCD最小的对角线系数
        #   [加乘后的最大公约数,加乘的倍数,要化简的行号,加乘的行号,要化简的列号]
        r = [self.mod, 1, i, i + 1, j]
        for k in xrange(i, self.r):
            for kk in xrange(k + 1, self.r):
                for l in range(j, self.c - 1):
                    rr = add_min_gcd(self.d[k][l], self.d[kk][l], self.mod)
                    if rr[0] < r[0]:
                        r[0] = rr[0]
                        r[1] = rr[1]
                        r[2] = k
                        r[3] = kk
                        r[4] = l
                        pass
                    if (1 == rr[0]):
                        break
        g = r[0]
        n = r[1]
        k = r[2]
        kk = r[3]
        l = r[4]

        if n and g < self.mod:
            self.d[k] = map(lambda x, y: (x + n * y) % self.mod, self.d[k], self.d[kk])
        return [k, l]

    def mul_row(self, i, k, j):
        a = self.d[k][j]
        b = self.d[i][j]

        def get_mul(a, b, m):
            k = gcd(a, m)
            if 1 == k:
                return mod_inv(a, m) * b % m
            else:
                if k == gcd(k, b):
                    return mod_inv(a / k, m / k) * (b / k) % (m / k)
            return None

        if b:
            mul = get_mul(a, b, self.mod)
            if None == mul:
                print_matrix(self.d)
                assert (mul != None)
            self.d[i] = map(lambda x, y: (y - x * mul) % self.mod, self.d[k], self.d[i])

    def gauss(self):
        """
        返回解向量，唯一解、多解或无解(None)。
        例如：[[61, 25, 116, 164], [61, 60, 116, 94], [61, 95, 116, 24], [61, 130, 116, 129], [61, 165, 116, 59]]
        """

        self.d = copy.deepcopy(self.matrix)
        for i in xrange(self.r):
            for j in xrange(self.c):
                self.d[i][j] = self.matrix[i][j] % self.mod  # 把负系数变成正系数

        if self.r < self.N:
            self.d.extend([[0] * self.c] * (self.N - self.r))

            # 化简上三角
        index = [x for x in xrange(self.N)]
        for i in range(self.N):
            tmp = self.find_min_gcd_row_col(i, i)
            if (tmp):
                self.swap_row(i, tmp[0])
                (index[i], index[tmp[1]]) = (index[tmp[1]], index[i])
                self.swap_col(i, tmp[1])
            else:
                self.error_str = "no min"
                return None

            for k in range(i + 1, self.r):
                self.mul_row(k, i, i)

        # print_matrix(self.d)
        if self.r > self.N:
            for i in xrange(self.N, self.r):
                for j in xrange(self.c):
                    if self.d[i][j]:
                        self.error_str = "r(A) != r(A~)"
                        return None

        # 判断解的数量
        for i in xrange(self.N):
            self.count *= gcd(self.d[i][i], self.mod)

        if self.count > 100:
            self.error_str = "solution too more:%d" % (self.count)
            return None

            # 回代
        result = [[None] * self.N]
        for i in range(self.N - 1, -1, -1):
            new_result = []
            for r in result:
                ret = self.inv_result(r, i)
                if ret:
                    for rr in ret:
                        l = r[:]
                        l[i] = rr
                        new_result.append(l)

                else:
                    self.error_str = "no inv:i=%d" % (i)
                    return None

            result = new_result

        # 调整列变换导致的未知数顺序变化
        for i in xrange(len(result)):
            def xchg(a, b):
                result[i][b] = a

            map(xchg, result[i][:], index)

        return result


###########################################################
# test
###########################################################
def print_array(x):
    prn = "\t["
    for j in x:
        if j:
            prn += "%3d, " % j
        else:
            prn += "  0, "

    print prn[:-2] + "],"


def print_matrix(x):
    print "["
    for i in x:
        print_array(i)
    print "]"


def random_test(times):
    import random
    for i in xrange(times):
        print "\n============== random test %d ==============\n" % i
        mod = random.randint(5, 999)
        col = random.randint(2, 30)
        row = random.randint(2, 30)

        solution = map(lambda x: random.randint(0, mod - 1), [xc for xc in xrange(col)])

        matrix = []
        for y in xrange(row):
            array = map(lambda x: random.randint(0, mod), [xc for xc in xrange(col)])

            t = 0
            for j in map(lambda x, y: 0 if None == y else x * y, array, solution):
                t += j
            array.append(t % mod)

            matrix.append(array)

        run_test(mod, solution, matrix)


def static_test_ex():
    mod = 37
    solution = [6, 10, 5, 11, 32, 39, 6, 42, 7, 18, 21, 8, 8, 27]
    matrix = [
        [32, 43, 11, 27, 14, 41, 27, 20, 0, 37, 7, 12, 9, 16, 12],
        [23, 35, 31, 25, 46, 27, 48, 0, 4, 19, 43, 11, 31, 24, 36],
        [48, 10, 47, 1, 42, 26, 0, 21, 10, 23, 7, 5, 13, 32, 41],
        [15, 0, 6, 24, 6, 36, 4, 36, 18, 46, 33, 20, 4, 20, 39],
        [4, 37, 3, 39, 26, 33, 13, 32, 23, 11, 45, 45, 29, 32, 35],
        [38, 8, 38, 47, 1, 34, 36, 46, 47, 0, 22, 23, 21, 31, 21],
        [21, 3, 17, 15, 46, 42, 7, 17, 12, 37, 30, 3, 14, 12, 16],
        [7, 22, 14, 31, 31, 19, 34, 46, 9, 33, 12, 18, 4, 15, 32],
        [13, 41, 35, 25, 19, 9, 44, 8, 0, 42, 15, 20, 3, 47, 29],
        [36, 21, 36, 13, 37, 40, 21, 39, 2, 16, 26, 4, 15, 2, 23],
        [41, 19, 28, 2, 42, 24, 27, 21, 21, 35, 3, 18, 7, 22, 36],
        [42, 34, 17, 40, 26, 7, 14, 0, 7, 46, 30, 14, 34, 22, 39],
        [18, 1, 40, 38, 17, 45, 24, 34, 34, 9, 32, 24, 9, 2, 45],
        [43, 2, 1, 29, 47, 48, 28, 37, 10, 23, 35, 34, 37, 44, 35],
    ]

    run_test(mod, solution, matrix)


def static_test():
    mod = 26
    solution = [23, 15, 19, 13, 25, 17, 24, 18, 11]
    matrix = [
        [11, 12, 7, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 11, 12, 7, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 11, 12, 7],
        [14, 18, 23, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 14, 18, 23, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 14, 18, 23],
        [17, 5, 19, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 17, 5, 19, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 17, 5, 19],
    ]

    for i in xrange(len(matrix)):
        t = 0
        for j in map(lambda x, y: 0 if None == y else x * y, matrix[i], solution):
            t += j
        matrix[i].append(t % mod)

    run_test(mod, solution, matrix)


def run_test(mod, solution, matrix):
    print "row = %d, col = %d" % (len(matrix), len(matrix[0]) - 1)
    print "mod = %d" % (mod)
    print "solution =", solution

    print "matrix ="
    print_matrix(matrix)

    g = GaussMatrix(matrix, mod)

    ret = g.gauss()
    if not ret:
        print "error:"
        print_matrix(g.d)
        print "error_str:", g.error_str
    else:
        print "times:", g.count
        print "result:"
        print_matrix(ret)


if __name__ == "__main__":
    data = []
    with open('/Users/wenhui/Downloads/bob_enc_5d6979d05829e676ea3154e4be14d553/out.txt') as f:
        for i in f.readlines():
            data.append(i)

    key = []
    eval('key.append({0})'.format(data[0]))
    key = key[0]

    s = []
    eval('s.append({0})'.format(data[1]))
    s = s[0]

    matrix = []
    tmp = []
    for i in range(len(key)):
        tmp = key[i]
        tmp.append(s[i])
        matrix.append(tmp)
    mod = 2141
    s = GaussMatrix(matrix, mod)
    flag1 = s.gauss()
    print flag1  # [[102, 108, 97, 103, 123, 49, 52, 101, 54, 102, 50, 51, 54, 45, 57, 101, 98, 57, 45, 52, 54]]

    for i in flag1:
        tmp = []
        for each in i:
            tmp.append(chr(each))
        print ''.join(tmp)
# [[102, 108, 97, 103, 123, 49, 52, 101, 54, 102, 50, 51, 54, 45, 57, 101, 98, 57, 45, 52, 54]]
# flag{14e6f236-9eb9-46

困惑于flag2的长度几何，以及噪声的消除方法

这里了解到了LWE

LWE问题

容错学习问题 （LWE问题， Learning With Errors）是一个机器学习领域中的怀疑难解问题，由Oded Regev 在2005年提出，他因此赢得2018年哥德尔奖。这是一个极性学习问题的一般形式。

但很可惜，一小时内没有成功利用之

比赛结束后，回到勇者山峰，发现密码也三道题了

• notKnapsack
• bob’s enc
• TrainPlus

传说殿堂也三道

• bob’s enc
• Train
• TrainPlus

总体而言，难度上，300分的notKnapsack = TrainPlus > bob’s enc >> Train

以及，传说殿堂远远没有勇者山峰卷🤔

后续再跟着其他师傅wp复现吧。

Bob’enc

以下为赛后复现，我决定尽可能多的挖掘此题价值

• 参考尚师傅博客

当时的困惑

• 题目生成列表时，行数列数究竟多少没看懂
• flag2多长
• LWE如何用

现在的未知

• 解题的矩阵思维
• sage命令背后的数学含义
• 过了几个月，学校教的线代已忘

先上师傅总的题解（…Orz

题解

# sage
from sage.all import *
from sage.modules.free_module_integer import IntegerLattice
from random import randint
import sys
from itertools import starmap
from operator import mul

with open('out', 'r') as f:
    key = eval(f.readline())
    c1 = eval(f.readline())
    c2 = eval(f.readline())

prime = 2141

K = matrix(Zmod(prime), key[:21])
C1 = vector(Zmod(prime), c1[:21])
m1 = K.inverse() * C1  # m1 = K\C1
flag = ''
for i in m1:
    flag += chr(i)
print(flag)


# Babai's Nearest Plane algorithm
def Babai_closest_vector(M, G, target):
    small = target
    for _ in range(5):
        for i in reversed(range(M.nrows())):
            c = ((small * G[i]) / (G[i] * G[i])).round()
            small -= M[i] * c
    return target - small


m = 64
n = 21
q = prime

A_values = key
b_values = c2

A = matrix(ZZ, m + n, m)
for i in range(m):
    A[i, i] = q
for x in range(m):
    for y in range(n):
        A[m + y, x] = A_values[x][y]
lattice = IntegerLattice(A, lll_reduce=True)

gram = lattice.reduced_basis.gram_schmidt()[0]
target = vector(ZZ, b_values)
res = Babai_closest_vector(lattice.reduced_basis, gram, target)

R = IntegerModRing(q)
M = Matrix(R, A_values)
ingredients = M.solve_right(res)

for i in ingredients:
    flag += chr(i)
print(flag)

flag1

C1 = multi(key, flag1)

对于multi，赛时我的理解是：单模多元线性同余方程

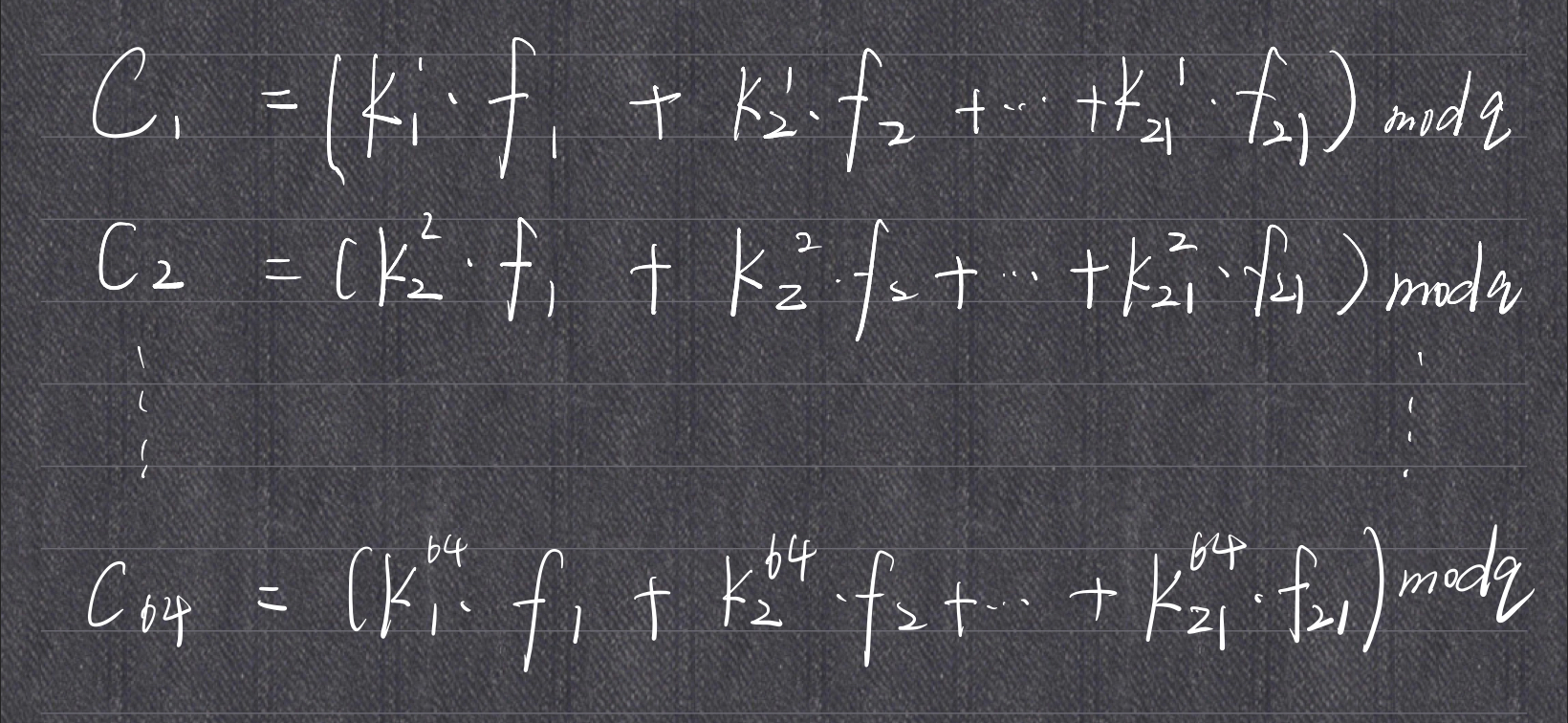
其中out里第一个大列表给了Key（所有ki）,第二个列表给了C1（上图左端所有C），所以我找到解此方程的代码，跑出来就是解了。

值得一提，看题目可知，这有64个方程，21个未知量，所以实际跑解方程的代码让C1 = C1[:21]也可

而在高深的密码人看来，C1是由定义在整数域上的p模环矩阵K 乘 向量F [f1, f2, …, f21]得到的：

矩阵K

[185  96 351 118 421 449 350 349 388  95 341 327  29 156 399 283 292 461 445 120 126]
[495 358 192 300 279 277 478 335 231 241 178 314 453 251 133 391 213 132 254 388  46]
[428  44 100 483  12 311  57 443 289  90 478 495 399  89 324 275 322  99 343 489 133]
[420 358 472 260 267 136 303 491 390 248 430 117 154 244  62 217 204 334 277 231 325]
[ 11  96  61  67 456 361 292 278 424 237 345 109 475 473  29 250 195 430 114  13 199]
[ 17  91 330  73 384 134 437 161 166 185 499 491 342 129 348 162 478 216 189 311 502]
[396 437  98 421 120 443 113 432   9 476 243 122 416 508 287  45  84 322 504 287 251]
[187 489 407 204 127  10 302 101 389 113 469 184 249 131 113  18 350 106 486 406 295]
[265 425  30 478 471 211 162 323 163 205 187 422 452 226 230 367 478 229 365 395 294]
[360 193 180 253 337 453  16 352 243 107 171  46  25 234  46 479 267 267 171 188 127]
[379 360 109 360 403 343  75 306 138  40  41 253 428 401 464 495  21 296 319 410 440]
[ 28 209   1 233 458 266 301 359 469 304 264 368 339  25 490 343 404 488 275 262 274]
[180 372 133 341  29 352 326  89 323 479  68  76 247 225 159 163 180 160 171   7 322]
[322 295  28 467 361 169 190  71 456 140 456 202 295 424 428  18 286 233 470 303 429]
[234  37 128 175 282 509  54 186 177  23 348 487 473 377  81 225 154 511 364 120 280]
[262  82 383 490 128 448 289 420 239 374 392 149 217 398 441 480 453 503 318 285 418]
[  0 347 223 381 469 208 424 435 404  64 107  73 490 116 445 392 194 287  66 325 261]
[ 99  26 489 114   3 351 494 174 369 354 379 187  90 202 286  37  48 397 298  65 499]
[455 114 349 401   5 139 314 227 134 258 270 135 287 332 298 272 167  43 271 484 177]
[448  78 479 324 170   7 230 173 214  65  91 497  68 391  44 205 364 471 460 312 122]
[452 360 448 169 240 496 302   3 354 266  46  22 151 498 461 314 169  88  30 487 258]

向量F

[102, 108, 97, 103, 123, 49, 52, 101, 54, 102, 50, 51, 54, 45, 57, 101, 98, 57, 45, 52, 54]

C1 = K✖️F

(1702, 795, 740, 373, 535, 1308, 1050, 502, 40, 672, 1354, 1843, 515, 231, 774, 65, 978, 1340, 455, 2137, 733)

经过验证，矩阵与向量相乘为每行对应项相乘再求和，以下

m = [102, 108, 97, 103, 123, 49, 52, 101, 54, 102, 50, 51, 54, 45, 57, 101, 98, 57, 45, 52, 54]
k = '185  96 351 118 421 449 350 349 388  95 341 327  29 156 399 283 292 461 445 120 126'.split(' ')
k = [int(i) for i in k if i]
sum = 0
for i in range(len(m)):
    sum += (m[i] * k[i]) % 2141
print(sum % 2141)
# 1702

故不用复杂的求解多个同余方程，可以直接让$K^{-1}*C1$，即可得到：F

• 注意，这里必须左乘$K^{-1}$,即：$C1 = KF; K^{-1}C1 = F$
  • 也就是说F是列向量？

from sage.all import *
from sage.modules.free_module_integer import IntegerLattice
from random import randint
import sys
from itertools import starmap
from operator import mul

with open('out', 'r') as f:
    key = eval(f.readline())
    c1 = eval(f.readline())
    c2 = eval(f.readline())

prime = 2141

#  矩阵求解的思维
K = matrix(Zmod(prime), key[:21])  # 一来，21行足够；二来方阵才可求逆
C1 = vector(Zmod(prime), c1[:21])
m1 = K.inverse() * C1
flag = ''
for i in m1:
    flag += chr(i)
print(flag)

整数域上的环，奇妙！

flag2

noise = [random.randint(0,6) for i in range(64)]

1. C2 = multi(Key, flag2)

2. C2 = add(noise, C2)

噪声打断了思绪，得重新整理整理。

赛时也了解到了LWE，但因为不知原理，不懂使用，故无所突破。

按照当时的想法，认为此法能消掉noise就很🐮了，但赛后发现可以直接给到flag2🐮🐮🐮

水平、时间有限，LWE系统的原理学习暂先搁置，先试着读读看使用方法与代码

简单翻译翻译，在此题中，则是给定Key矩阵，先令矩阵Key*向量flag2后再与noise相加，故：

• A = Key
• s = flag2
• e = noise
• b = C2

而LWE问题就是给A、b, 求s

所以一开始所惊叹的‘能直接求出flag2’，在此印证

#脚本2-大规模
#Sage
from sage.modules.free_module_integer import IntegerLattice
from random import randint
import sys
from itertools import starmap
from operator import mul

# Babai's Nearest Plane algorithm
# from: http://mslc.ctf.su/wp/plaidctf-2016-sexec-crypto-300/
def Babai_closest_vector(M, G, target):
    small = target
    for _ in range(1):
        for i in reversed(range(M.nrows())):
            c = ((small * G[i]) / (G[i] * G[i])).round()
            small -= M[i] * c
    return target - small

# A一般为key
# b为密文
# e为噪声
# s为flag（下面的ingredients
  
m =   # A行数
n =   # A列数
q =   # 模数

A_values = 
b_values = 

A = matrix(ZZ, m + n, m)
for i in range(m):
    A[i, i] = q
for x in range(m):
    for y in range(n):
        A[m + y, x] = A_values[x][y]
lattice = IntegerLattice(A, lll_reduce=True)
print("LLL done")
gram = lattice.reduced_basis.gram_schmidt()[0]
target = vector(ZZ, b_values)
res = Babai_closest_vector(lattice.reduced_basis, gram, target)
print("Closest Vector: {}".format(res))

R = IntegerModRing(q)
M = Matrix(R, A_values)
ingredients = M.solve_right(res)

print("Ingredients: {}".format(ingredients))

for row, b in zip(A_values, b_values):
    effect = sum(starmap(mul, zip(map(int, ingredients), row))) % q
    assert(abs(b - effect) < 2 ** 37)

print("ok")

也发现，我们不需要知道flag2的长度

收获

• 矩阵、向量解题思路
• LWE消除噪音
• 加深对sage的了解