Harry's Blog

温故知新

0%

数学概念的Sage实现

发表于 更新于   阅读次数： Valine：
本文字数： 5.7k 阅读时长 ≈ 5 分钟
密码学中SageMath应用指南

数学概念的sage实现

第一次学习，参考la佬博客Orz

la佬写的精简干练，一度以为不是在记笔记而是转载XD

第二次完善，拜读V神的文章

第三次总结，研读sage中文文档 & Sage Quick Reference: Linear Algebra

gmpy2

gmpy2 是python里一个优秀的数论相关库

1
2
3
4
5
6
7
8
9
import gmpy2
gmpy2.mpz(n)	#初始化一个大整数
gmpy2.mpfr(x)	# 初始化一个高精度浮点数x
d = gmpy2.invert(e,n) 	# 求逆元，de = 1 mod n
c = gmpy2.powmod(m,e,n)	# 幂取模，结果是 c = m^e mod n
gmpy2.is_prime(n)	 #素性检测
gmpy2.gcd(a,b)  	#欧几里得算法，最大公约数
gmpy2.gcdext(a,b)  	#扩展欧几里得算法
gmpy2.iroot(x,n) 	#x开n次根

陌生

  • gmpy2.mpz(n) #初始化一个大整数
  • gmpy2.mpfr(x) # 初始化一个高精度浮点数x

Sage

R.<X> = PolynomialRing(Zmod(n))

  • Zmod(n):

    • n: 指定模为n的环
    • Z: 表示整数

    有效的数字只有从0到n，其他的都通过与n取模来保证在0～n这个范围内

  • 参数介绍

    • ZZ：整数环
    • QQ: 有理数环
    • RR：实数环
    • CC：复数环

  • PolynomialRing

    建立多项式环

  • R

    指针，指向用PolynomialRing指定的那个环.

    实际上用什么字母都可以

  • .<X>

    指定一个变量

数论相关

1
2
3
4
5
6
7
8
9
10
11
prime_pi(n)  #小于等于n的素数个数
divisors(n)  #n的因子
number_of_divisors(n)  #n的因子总数
factor(n)  #n的因式分解
euler_phi(n)  #n的欧拉函数值
three_squares(n)  #n的三数平方组合
four_squares(n)  #n的四数平方组合

d = inverse_mod(e,fn) # sage求e对模fn的逆元d
d,u,v=xgcd(20,30)  # 扩展欧几里得算法
# d = gcd(20,30) = 20*u + 30*v

陌生

  • prime_pi(n)

  • divisors(n) and number_of_divisors(n)

  • three_squares(n) and four_squares(n)

    1
    2
    3
    4
    5
    print(three_squares(78))
    # (2, 5, 7)

    print(four_squares(78))
    # (1, 2, 3, 8)

factor

1
2
3
4
5
6
7
ms = [284461942441737992421992210219060544764, 218436209063777179204189567410606431578,
      288673438109933649911276214358963643204, 239232622368515797881077917549177081575,
      206264514127207567149705234795160750411, 338915547568169045185589241329271490503,
      246545359356590592172327146579550739141, 219686182542160835171493232381209438048]
for i in ms:
    print(factor(i))
    print(factor(i)[0])

输出

(a, b)

  • a为底数
  • b为幂
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2^2 * 7 * 11 * 37 * 4931 * 68447 * 19044797 * 3883344883673875271
(2, 2)
2 * 23 * 430811 * 145978487 * 6348599837 * 11893596584627
(2, 1)
2^2 * 11 * 6560759957043946588892641235430991891
(2, 2)
3^2 * 5^2 * 359 * 790756753 * 3745419995624210070676241
(3, 2)
593 * 1037401 * 16138908347 * 20775381485756890441
(593, 1)
3 * 11 * 19 * 835427 * 647016631717189608780181516607
(3, 1)
53 * 6189511 * 10973906636081 * 68486246189098967
(53, 1)
2^5 * 3 * 17 * 109 * 148008571 * 689385523 * 12103391051447837
(2, 5)

它不是查询，sage会正儿八经地给你跑算法拆n

多项式

  • 杂

    • f.subs({x:x1})

      把x1值代入x

    • f.univariate_polynomial()

      univariate单变量的，映射为单变量多项式

    • f.univariate_polynomial().roots()

      单变量多项式求根

    • f.coefficients()

      coefficient系数，多项式系数列表

    • f.monic()

      monicpolynomial首个系数为1的多项式

  • 单元·因式分解

    1
    2
    3
    4
    5
    6
    x = PolynomialRing(RationalField(), 'x').gen()
    # RationalField有理域

    f = (x^3 - 1)^2-(x^2-1)^2
    f.factor()
    # (x - 1)^2 * x^2 * (x^2 + 2*x + 2)

  • 二元·因式分解

    1
    2
    3
    4
    5
    x, y = PolynomialRing(RationalField(), 2, ['x','y']).gens()
    f =  (9*y^6 - 9*x^2*y^5 - 18*x^3*y^4 - 9*x^5*y^4 + 9*x^6*y^2 + 9*x^7*y^3 + 18*x^8*y^2 - 9*x^11)
    f.factor()

    # (9) * (-x^5 + y^2) * (x^6 - 2*x^3*y^2 - x^2*y^3 + y^4)

  • 单元·GCD

    1
    2
    3
    4
    5
    6
    x = PolynomialRing(RationalField(), 'x').gen()
    f = 3*x^3 + x
    g = 9*x*(x+1)
    f.gcd(g)

    # x

  • 多元·GCD

    1
    2
    3
    4
    5
    6
    R.<x,y,z> = PolynomialRing(RationalField(), order='lex')
    f = 3*x^2*(x+y)
    g = 9*x*(y^2 - x^2)
    f.gcd(g)

    # x^2 + x*y

矩阵

  • 矩阵的定义

    • A = matrix(定义域, 值)

      1
      2
      3
      4
      5
      6
      A = matrix(ZZ, [[1,1],[0,4]])
      # 创建了定义域在整数环的矩阵
      """
      [[1, 1]
       [0, 4]]
      """

      也可以交代清楚指定的行数与列数

      1
      2
      3
      F1=matrix(QQ,2,2,[0,1,1,0])
      [0,1]
      [1.0]

  • 列向量置入定义

    每个向量以列向量的形式置入矩阵

    1
    2
    3
    4
    sage: column_matrix(QQ,[[1,2,3],[4,5,6],[7,8,9]])
    [1 4 7]
    [2 5 8]
    [3 6 9]

  • 矩阵组合定义

    1
    2
    3
    4
    5
    6
    7
    8
    sage: F1=matrix(QQ,2,2,[0,1,1,0])
    sage: F2=matrix(QQ,2,2,[1,2,3,4])
    sage: F3=matrix(QQ,1,2,[3,1])
    sage: block_matrix(2,2,[F1,F2,0,F3])
    [0 1|1 2]
    [1 0|3 4]
    [---+---]
    [0 0|3 1]

  • 向右生长

    1
    2
    3
    sage: F1.augment(F2)
    [0 1 1 2]
    [1 0 3 4]

  • 向下生长

    1
    2
    3
    4
    5
    sage: F1.stack(F2)
    [0 1]
    [1 0]
    [1 2]
    [3 4]

  • 以块为单位的对角阵

    1
    2
    3
    4
    5
    6
    sage: block_diagonal_matrix([F1,F2])
    [0 1|0 0]
    [1 0|0 0]
    [---+---]
    [0 0|1 2]
    [0 0|3 4]

  • 矩阵属性

    • A.nrows()

      矩阵行数

    • A.ncols()

      矩阵列数

    • V.dimension()

      查看v矩阵的维度

    • A.transpose()

      转置

      矩阵转置

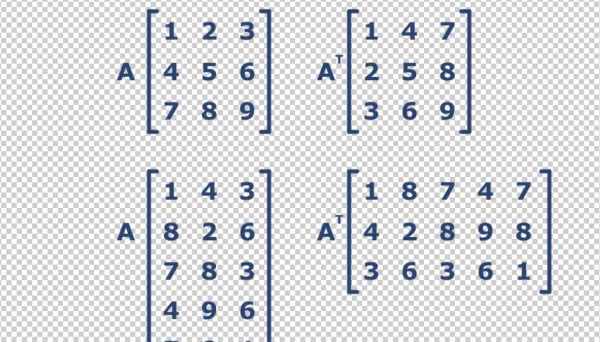
    • A.inverse()

      矩阵的逆

    • A.rank()

      矩阵的秩

    • A.det()

      将矩阵转换为行列式

    • A.stack(vector([1,2]))

      矩阵末添加一行（向量）

    • A.insert_row(n, vector([1,2]))

      在矩阵第n行插入（向量）

    • A.change_ring(QQ)

      更换环为QQ（有理数环）

    • A.solve_left(B) 或A/B

      求解XA=B

    • A.solve_right(B) 或 A\B

      求解AX=B

    • A.left_kernel()

      求解XA=0，线性相关的行向量

    • A.right_kernel()
      解AX=0，线性相关的行向量

    • A.LLL()

      LLL算法求最短正交基

    • A.multiplicative_order()

      乘法阶

  • 特别的

    • zero_matrix(2,3)

      创建（2*3）零矩阵

    • identity_matrix(2,3)

      创建（2*3）单位阵

    • block_matrix(QQ,[[Matrix_A,Matrix_B],[matrix(C),matrix(D)]])

      矩阵拼接

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      A = matrix(ZZ, [[1,1],[0,4]])
      b = [[2,2],[3,3]]
      n = 2

      block_matrix(QQ,[[A,zero_matrix(n,2)],[matrix(b),matrix([[4,4],[5,5]])]])
      """
      [1 1|0 0]
      [0 4|0 0]
      [---+---]
      [2 2|4 4]
      [3 3|5 5]
      """

困惑

  • 关于$matrix()vector()$, *sage是会自动变向量为列向量或行向量来使得乘法可算吗？**

    查阅中文文档后，证实Sage为了让乘法合理化，会尽可能调整向量是行或列向量。

    而在使用之前，向量的状态是混沌的。

求解方程

普通方程

$\left\{\begin{aligned}x+y&=10\\xy&=21\end{aligned}\right.$

1
2
var('x y')  # 申明变量
solve([x+y==10, x*y==21], [x,y])  # 求解

线性方程组

1
2
3
4
5
6
A = Matrix([[1,2,3],[3,2,1],[1,1,1]]) 
Y = vector([0,-4,-1]) 
X = A.solve_right(Y)
#或
A \ Y
#反斜杠 \ 可以代替 solve_right; 用 A \ Y 代替 A.solve right(Y).
  • 给一个记忆点，斜杠的下端在哪边，未知量x就在哪边

RSA相关方程

$\left\{\begin{aligned}N&=pq\\ \phi &= (p-1)(q-1)\end{aligned}\right.$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
P.<p, q> = PolynomialRing(ZZ)
def solve(f1, f2):
	g = f1.resultant(f2, q)
	roots = g.univariate_polynomial().roots()
	if len(roots) == 0:
		return False
	p_ = abs(roots[0][0])
	q_ = abs(roots[1][0])
	return (min(p_, q_), max(p_, q_))

N = 
phi = 
f1 = (N + 1) - phi - p - q
f2 = N - p*q
p, q = solve(f1, f2)
(p, q)

CRT(中国剩余定理)

$\left\{\begin{aligned}x&≡2 (mod3)\\x&≡3(mod5)\\x&≡2(mod7)\end{aligned}\right.$

Sage内置CRT函数crt([2,3,2], [3,5,7])

但没有模不互素的扩展中国定理excrt（具体原理、代码可见我的博客中Crypto常见算法一文）

离散对数

$a^x ≡ b (\mod n )$

  • n为合数

    利用Pohlig-Hellman算法（后续再补充原理学习）

    x = discrete_log(mod(b,n),mod(a,n))

    ??? n是质数幂也解出来了

  • n为质数或质数幂

    线性筛Index Calculus方法（不了解）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    R = Integers(99)
    a = R(4)
    b = a^9
    b.log(a)
    # 9 

    # 或
    x = int(pari(f"znlog({int(b)},Mod({int(a)},{int(n)}))"))
    x = gp.znlog(b, gp.Mod(a, n))

椭圆曲线

$y^2 =x^3 + ax + b$

  • F = GF(7)

    素数域

  • F.order()

    素数域的阶

  • E = EllipticCurve(F,[0,0,0,2,3])

    定义椭圆曲线$F_7(2,3)$

  • G = E.gens()[0]

    基点坐标

  • q = E.order()
    阶

  • allPoints = E.points()
    所有的点

  • P = E(2,1)
    创建点

  • P.xy()
    点的xy坐标

结式¶

1
2
3
4
5
6
7
8
9
10
11
12
from sage.matrix.matrix2 import Matrix
def resultant(f1, f2, var):
    return Matrix.determinant(f1.sylvester_matrix(f2, var))

n = 
P.<k,t2,t3,d> = PolynomialRing(Integers(n))
f1 = s1*k - h - r*d
f2 = s2*(k+t2) - h - r*d
f3 = s3*(k+t3) - h - r*d
h1 = resultant(f1, f2, d)
h2 = resultant(f1, f3, d)
g1 = resultant(h1, h2, k)

结式求解

1
2
3
4
f = f1.resultant(f2, xp)  # 消xp
PR.<p>=PolynomialRing(ZZ)
f = f(p, p)  # 转换为单元多项式
p = f.roots()[0][0]