Crypto_easy_crypto | N中有大合数
题目
1 | from Crypto.Util.number import * |
题解
1 | import libnum |
直接把另一堆(p*q*r)忽略了,当成单素数(p+q+r)加密的RSA解🤔
回想起来,原来看过此类问题的解法视频
可惜,被p、q、r唬住了。
结论
- N分解过程中,比m大的合数可以直接忽略
- 剩下的也不一定是素数,记得check
- 剩下的数当作新的模,得大于m(不然就得爆破k)
为什么?不知道
CRT | 共d
题目
1 | from Crypto.Util.number import * |
题解
1 | ###Sage### |
或许非预期吧,直接把d用LLL算法求出来了。
结论
- 共d用LLL算法攻击(记得
d = abs(Mat_LLL[0][0])// M整除!
crtrsa | dp小,e 很大
题目
1 | from secret import flagn,p,q |
可以看到dp的范围是在[1,1048576],这个范围应该是可以进行穷举的 -> dp已知
题解
1 | import gmpy2 |
总结
因 e⋅dp≡1(mod(p−1)),又由费马小定理,对r (大于1的整数 且 gcd(p, r)=1),有 $r^{e⋅dp} ≡ r (modp)$,即 $p | (r^{e⋅dp} − r)$;
又 p | n,很大概率 $p=gcd(r^{e·dp} − r, n)$
- 当dp较小且已知,e又较大时,对任意 m,$p=gcd(r^{e·dp} − r, n)$
Easy_Rsa | p-1、q-1有公因子
题目
1 | from Crypto.Util.number import * |
题解
1 | # Pollard’s rho |
总结
Common Prime RSA
情形:gcd(p−1,q−1)=g
分解的n方法有四种:
(1)修改Pollard’s rho方法分解n;
(2)知道a、b的值分解n;
(3)知道g的值分解n;
(4)分解N-1。
baby_rsa |$p, q=v_i^{m_i+1}−(v_i+1)^{m_i}$
题目
1 | #!/usr/bin/env python3 |
题解
en1
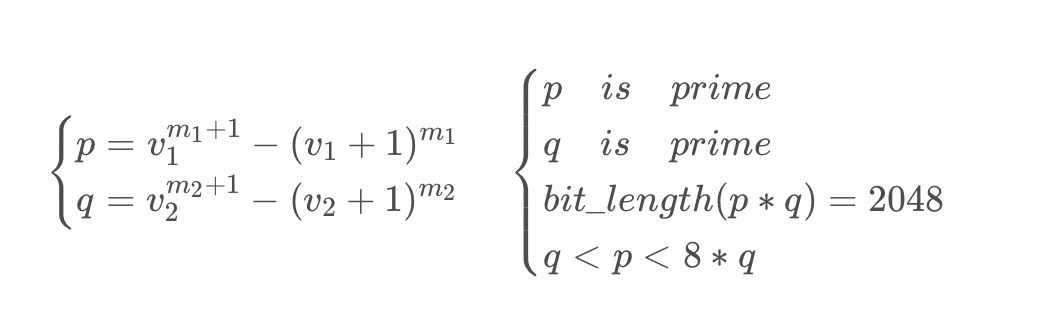
p,q的比特长度均小于2048(应该更小)。我们可以通过这个条件来枚举v和m,求出该范围内的所有素数,然后再从中选取任意两个素数,求n,长度若为2048bits,则尝试解密。
1 | import gmpy2 |
en2
2
3
4
5
6
7
8
9
c2, n2, p = (40625981017250262945230548450738951725566520252163410124565622126754739693681271649127104109038164852787767296403697462475459670540845822150397639923013223102912674748402427501588018866490878394678482061561521253365550029075565507988232729032055298992792712574569704846075514624824654127691743944112075703814043622599530496100713378696761879982542679917631570451072107893348792817321652593471794974227183476732980623835483991067080345184978482191342430627490398516912714451984152960348899589532751919272583098764118161056078536781341750142553197082925070730178092561314400518151019955104989790911460357848366016263083, 43001726046955078981344016981790445980199072066019323382068244142888931539602812318023095256474939697257802646150348546779647545152288158607555239302887689137645748628421247685225463346118081238718049701320726295435376733215681415774255258419418661466010403928591242961434178730846537471236142683517399109466429776377360118355173431016107543977241358064093102741819626163467139833352454094472229349598479358367203452452606833796483111892076343745958394932132199442718048720633556310467019222434693785423996656306612262714609076119634814783438111843773649519101169326072793596027594057988365133037041133566146897868269, 39796272592331896400626784951713239526857273168732133046667572399622660330587881579319314094557011554851873068389016629085963086136116425352535902598378739)
print(gmpy2.is_prime(p))
print(p)
phi2 = (191-1)*(193-1)*(627383-1)*(1720754738477317127758682285465031939891059835873975157555031327070111123628789833299433549669619325160679719355338187877758311485785197492710491-1)
d2 = int(gmpy2.invert(e2, phi2))
m2 = pow(c2, d2, p)
print(long_to_bytes(m2))
# #b'42-b659-0c96ef827f05}'舍掉合数
值得注意,剩下的居然还是个合数,得拆了求其phi
总结
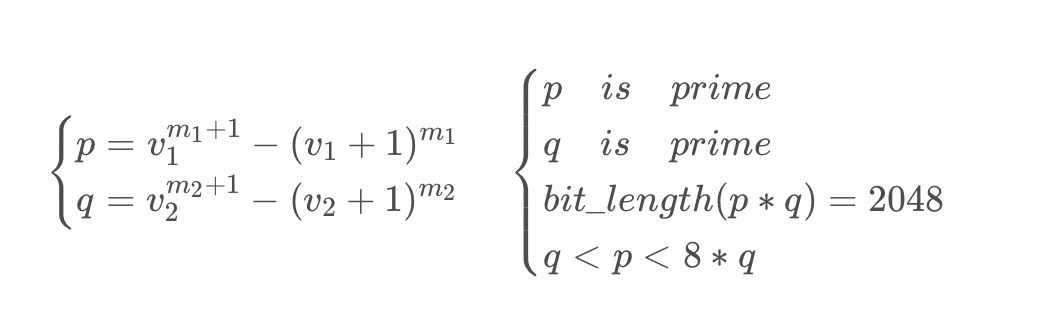
- 穷举所有v,m(即穷举所有p、q)
special_rsa | (e|p-1) & (e|q-1)
有限域开e次方,解决问题。
但e不能太大🤔
1 | #脚本2 |
总结
- (e|p-1) & (e|q-1), AMM算法解决
CVE OF RSA |p=km+(65537*a % n)
题目
1 | def special_rsa(self): |
总结
babyrsa |低加密指数广播攻击
题目
1 | n = [] |
题解
1 | def CRT(cl, nl): |
总结
- $m^e ≡ c \mod(n)$ 由CRT得$m^e$,开e次方即解
Rabin |模4不余3
1 | from Crypto.Util.number import getPrime |
n次同余方程
1 | from Crypto.Util.number import getPrime |
Swedish RSA |多项式RSA
有限域上的多项式
- 有限域:有限个数的集合
- 有限域多项式:系数属于某个有限域的多项式
- 有限域下不可约多项式:一个多项式不能被拆成多个同一有限域下多个多项式的乘积
加解密
对系数定义在GF(p)上的多项式N
拆解之,得到多项式P、Q
即:N = P * Q
计算N的欧拉函数phi
如何求phi
记在GF(p)上, X的最高次数为a,则:
$$\phi (X) = p^a - 1$$
即:$$\phi (N) = \phi (P) * \phi (Q) = (p^{P.degree()}-1)*(p^{Q.degree()}-1)$$
选一个整数e,(e, phi)=1,并求出逆元d,e×d≡1(mod phi)
加密:$$C= M^e \mod N$$
解密:$$M = C^d \mod N$$
明文转换成多项式
- 将明文每个字符转ascii,作为多项式m的系数
其中e和d都是整数,它们和多项式可以进行模幂运算
题解
1 | #!/usr/bin/env sage |
unusualrsa2 |线性关系Franklin-Reiter攻击
一言以蔽之,利用多项式gcd得到最大公因子$x-M$
其中e=3的证明情况见CTF-Wiki,更全面的看上面论文
题目
1 | # ******************** |
解题脚本
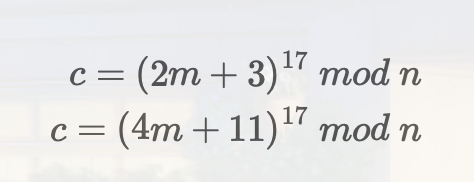
1 | #脚本1 |
unusuarsa4 |inv(q,p),c,d;没n
- 参考博客(4xwill师傅yyds
题目
1 | # ******************** |
题解
理论推理
- hint1: $$inv(q, p) · phi \mod p$$
- hint2:
- 费马小定理
- 给定r, k1, k2,若 k2|k1,则:$r \mod k2 = (r \mod k1) \mod k2$
记inv(q, p) = q1, 题目给了q1,那么有如下性质:
$$q1* q ≡ 1 \mod p$$
构造hint1的格式:
$$q1•phi ≡ q1•(p-1)•(q-1) ≡ (p-1)•(q1•q - q1) ≡ (p-1) (1-q1) ≡ (1-q1) \mod p$$
即:
$$q1•phi + q1 -1 = k•p$$
记kp = q1*phi + q1 -1 ,则:p | kp
接下来,聚焦hint2,任选满足$gcd(g, p) = 1$的g, 则:
$$g^{phi} ≡ 1 \mod n$$ —> $$g^{phi} ≡ 1 \mod p$$ —> $$(g^{phi} \mod kp) ≡ 1 \mod p$$
即:
$$p |(g^{phi} \mod kp) - 1$$
解题思路
知道e、d,则:$e*d -1 = k’ * phi$
利用此,爆破phi
用爆破出的phi计算kp
任选两个素数g1, g2(这样有gcd(g, p) =1)
计算出x1 = $(g_1^{phi} \mod kp) -1$, x2 = $(g_2^{phi} \mod kp) -1$
易得:p = gcd(x1, x2)
由phi、p得q、n
RSA解密
1 | import libnum |
unusualrsa1 |m高位泄漏
1 | # ******************** |
题解
m高位泄漏
1 | # sage |
[长安杯 2021]checkin |威尔逊定理
题目
1 | from Crypto.Util.number import * |
题解
前置知识
威尔逊定理:
对于素数p有充分必要条件:
$$(p-1)! ≡ -1 \mod p$$
聚焦题目,已知:
- $$c1 = 2^e \mod n$$
- $$c2 = m^{e} \mod n$$
- e = 1049
利用 1 ,得到:$c1 - 2^e = k*n$
分解$c1-2^e$再根据位数,得到p、q
解出m_(此m_显然不是flag对应的long型数字
1 | import gmpy2 |
看题目代码里,唯一复杂的部分:
1 | for i in range(1,p-q): |
以下,推理其性质
$$m_0$$(flag对应的)
$$m1 = (m_0 * 1) \mod n$$
$$m2 = (((m_0 * 1)\mod n) *2) \mod n = (m_0 * 1 *2) \mod n$$
$$ m3 = (((m_0 * 1 2)\mod n)3) \mod n = (m_0 * 1 *2 *3) \mod n$$
…
$$m_n = (m_0 * p!) \mod n$$
实际做题时,就是看到阶乘才知道利用威尔逊定理
由题目,得:
m_ = $$(m_0 * (p-q-1)!) \mod n$$
等号是兼容同余的,由同余性质9有:m_ $≡ (m_0 * (p-q-1)!) \mod p$
则,有:m_ $= (m_0 * (p-q-1)!) \mod p$
为使用威尔逊定理,构造出p!
$(m\_ • [(p-q)•(p-q+1)•…•(p-1)] ) \mod p = m_0•(p-1)! \mod p$
由威尔逊定理,得:$(m\_• [(p-q)•(p-q+1)•…•(p-1)]) \mod p = m_0•(p-1)! \mod p = -m_0 \mod p$
那么,m0 = (inv(-1, p)*m_ * [(p-q)*(p-q+1)*...*(p-1)]) mod p + k*p
这里另一个难题是,求m_ * ([p-q)*(p-q+1)*...*(p-1)]) mod p)
其实,利用题目的给的格式即可求得,然后爆破m0,解出flag
1 | for i in range(p-q, p): |
总代码
1 | import gmpy2 |
boneh_durfee |e大d小
题目
1 | from Crypto.Util.number import bytes_to_long, long_to_bytes, getPrime |
题解
e非常非常大,我的本能是Wiener attack.
实际跑起来,说无解,看来不适用。
n也拆不出来
搜索题目
boneh_durfee,找到F2X师傅师傅给的脚本,跑出了私钥dd = 16047294678407380708470035960641178683792869987929646123144231278863168786312071
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335import time
"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = True
"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False
"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension
############################################
# Functions
##########################################
# display stats on helpful vectors
def helpful_vectors(BB, modulus):
nothelpful = 0
for ii in range(BB.dimensions()[0]):
if BB[ii,ii] >= modulus:
nothelpful += 1
print (nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")
# display matrix picture with 0 and X
def matrix_overview(BB, bound):
for ii in range(BB.dimensions()[0]):
a = ('%02d ' % ii)
for jj in range(BB.dimensions()[1]):
a += '0' if BB[ii,jj] == 0 else 'X'
if BB.dimensions()[0] < 60:
a += ' '
if BB[ii, ii] >= bound:
a += '~'
print (a)
# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):
# end of our recursive function
if current == -1 or BB.dimensions()[0] <= dimension_min:
return BB
# we start by checking from the end
for ii in range(current, -1, -1):
# if it is unhelpful:
if BB[ii, ii] >= bound:
affected_vectors = 0
affected_vector_index = 0
# let's check if it affects other vectors
for jj in range(ii + 1, BB.dimensions()[0]):
# if another vector is affected:
# we increase the count
if BB[jj, ii] != 0:
affected_vectors += 1
affected_vector_index = jj
# level:0
# if no other vectors end up affected
# we remove it
if affected_vectors == 0:
print ("* removing unhelpful vector", ii)
BB = BB.delete_columns([ii])
BB = BB.delete_rows([ii])
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii-1)
return BB
# level:1
# if just one was affected we check
# if it is affecting someone else
elif affected_vectors == 1:
affected_deeper = True
for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
# if it is affecting even one vector
# we give up on this one
if BB[kk, affected_vector_index] != 0:
affected_deeper = False
# remove both it if no other vector was affected and
# this helpful vector is not helpful enough
# compared to our unhelpful one
if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):
print ("* removing unhelpful vectors", ii, "and", affected_vector_index)
BB = BB.delete_columns([affected_vector_index, ii])
BB = BB.delete_rows([affected_vector_index, ii])
monomials.pop(affected_vector_index)
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii-1)
return BB
# nothing happened
return BB
"""
Returns:
* 0,0 if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
"""
Boneh and Durfee revisited by Herrmann and May
finds a solution if:
* d < N^delta
* |x| < e^delta
* |y| < e^0.5
whenever delta < 1 - sqrt(2)/2 ~ 0.292
"""
# substitution (Herrman and May)
PR.<u, x, y> = PolynomialRing(ZZ)
Q = PR.quotient(x*y + 1 - u) # u = xy + 1
polZ = Q(pol).lift()
UU = XX*YY + 1
# x-shifts
gg = []
for kk in range(mm + 1):
for ii in range(mm - kk + 1):
xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk
gg.append(xshift)
gg.sort()
# x-shifts list of monomials
monomials = []
for polynomial in gg:
for monomial in polynomial.monomials():
if monomial not in monomials:
monomials.append(monomial)
monomials.sort()
# y-shifts (selected by Herrman and May)
for jj in range(1, tt + 1):
for kk in range(floor(mm/tt) * jj, mm + 1):
yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)
yshift = Q(yshift).lift()
gg.append(yshift) # substitution
# y-shifts list of monomials
for jj in range(1, tt + 1):
for kk in range(floor(mm/tt) * jj, mm + 1):
monomials.append(u^kk * y^jj)
# construct lattice B
nn = len(monomials)
BB = Matrix(ZZ, nn)
for ii in range(nn):
BB[ii, 0] = gg[ii](0, 0, 0)
for jj in range(1, ii + 1):
if monomials[jj] in gg[ii].monomials():
BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)
# Prototype to reduce the lattice
if helpful_only:
# automatically remove
BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)
# reset dimension
nn = BB.dimensions()[0]
if nn == 0:
print ("failure")
return 0,0
# check if vectors are helpful
if debug:
helpful_vectors(BB, modulus^mm)
# check if determinant is correctly bounded
det = BB.det()
bound = modulus^(mm*nn)
if det >= bound:
print ("We do not have det < bound. Solutions might not be found.")
print ("Try with highers m and t.")
if debug:
diff = (log(det) - log(bound)) / log(2)
print ("size det(L) - size e^(m*n) = ", floor(diff))
if strict:
return -1, -1
else:
print ("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")
# display the lattice basis
if debug:
matrix_overview(BB, modulus^mm)
# LLL
if debug:
print ("optimizing basis of the lattice via LLL, this can take a long time")
BB = BB.LLL()
if debug:
print ("LLL is done!")
# transform vector i & j -> polynomials 1 & 2
if debug:
print ("looking for independent vectors in the lattice")
found_polynomials = False
for pol1_idx in range(nn - 1):
for pol2_idx in range(pol1_idx + 1, nn):
# for i and j, create the two polynomials
PR.<w,z> = PolynomialRing(ZZ)
pol1 = pol2 = 0
for jj in range(nn):
pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)
pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)
# resultant
PR.<q> = PolynomialRing(ZZ)
rr = pol1.resultant(pol2)
# are these good polynomials?
if rr.is_zero() or rr.monomials() == [1]:
continue
else:
print ("found them, using vectors", pol1_idx, "and", pol2_idx)
found_polynomials = True
break
if found_polynomials:
break
if not found_polynomials:
print ("no independant vectors could be found. This should very rarely happen...")
return 0, 0
rr = rr(q, q)
# solutions
soly = rr.roots()
if len(soly) == 0:
print ("Your prediction (delta) is too small")
return 0, 0
soly = soly[0][0]
ss = pol1(q, soly)
solx = ss.roots()[0][0]
#
return solx, soly
def example():
############################################
# How To Use This Script
##########################################
#
# The problem to solve (edit the following values)
#
# the modulus
N = 116619053095181844867756588238123176803022888638090603550604610234584486986893904698844566541567093613495764007369858037838298617868152946508912345019503344911355228396374219771717648337137214599383155473846763062399405332170035904047911459812639096963243997609662442560069465026848168759806881590989694374289
# the public exponent
e = 28366532045084591636437544767374939012961757129620507106907154467035496029282857415182567552270978206397793889819857945701555381457862312304572366567535998525153574576210520634959025982966194022680398054500011866734299857844098161391787585786609289654556120958843118695788794035767689727287572845453232286487
# the hypothesis on the private exponent (the theoretical maximum is 0.292)
delta = 0.280 # this means that d < N^delta
#
# Lattice (tweak those values)
#
# you should tweak this (after a first run), (e.g. increment it until a solution is found)
m = 4 # size of the lattice (bigger the better/slower)
# you need to be a lattice master to tweak these
t = int((1-2*delta) * m) # optimization from Herrmann and May
X = 2*floor(N^delta) # this _might_ be too much
Y = floor(N^(1/2)) # correct if p, q are ~ same size
#
# Don't touch anything below
#
# Problem put in equation
P.<x,y> = PolynomialRing(ZZ)
A = int((N+1)/2)
pol = 1 + x * (A + y)
#
# Find the solutions!
#
# Checking bounds
if debug:
print ("=== checking values ===")
print ("* delta:", delta)
print ("* delta < 0.292", delta < 0.292)
print ("* size of e:", int(log(e)/log(2)))
print ("* size of N:", int(log(N)/log(2)))
print ("* m:", m, ", t:", t)
# boneh_durfee
if debug:
print ("=== running algorithm ===")
start_time = time.time()
solx, soly = boneh_durfee(pol, e, m, t, X, Y)
# found a solution?
if solx > 0:
print ("=== solution found ===")
if False:
print ("x:", solx)
print ("y:", soly)
d = int(pol(solx, soly) / e)
print ("private key found:", d)
else:
print ("=== no solution was found ===")
if debug:
print("=== %s seconds ===" % (time.time() - start_time))
if __name__ == "__main__":
example()
rsa解密,得到flag
1
2
3
4
5
6
7
8
9import libnum
d = 1604729467840738070847003596064117868379286998792964612314423127886316878631207
e= 28366532045084591636437544767374939012961757129620507106907154467035496029282857415182567552270978206397793889819857945701555381457862312304572366567535998525153574576210520634959025982966194022680398054500011866734299857844098161391787585786609289654556120958843118695788794035767689727287572845453232286487
n = 116619053095181844867756588238123176803022888638090603550604610234584486986893904698844566541567093613495764007369858037838298617868152946508912345019503344911355228396374219771717648337137214599383155473846763062399405332170035904047911459812639096963243997609662442560069465026848168759806881590989694374289
c = 5550387375810892705924800464945980988431639193797468627845836397962361427321133854633770242318969576163563079147919098794998899335191281861385800469677049957403290859349688725585260874592933564793273307183923684839207469443101629472424936878786558261355723914033881683475668259544365455286750343306090149047
m = int(pow(c, d, n))
print(libnum.n2s(m))
# b"novaCTF{d0n't_J0_kn0wn_b0n3h_durf33}"
总结
e过大求解再添一员猛将
e 非常大接近于N,即 d 较小时。与低解密指数攻击类似,比低解密指数攻击(Wiener Attack)更强,可以解决$\frac{1}{3} N^{\frac{1}{4}} ≤ d ≤ N^{0.292}$的问题。
- 若 $d < \frac{1}{3} N^{\frac{1}{4}}$ ,则可选择Winner攻击
- 若$\frac{1}{3} N^{\frac{1}{4}} ≤ d ≤ N^{0.292}$,则可选择Boneh和Durffe攻击攻击
Pohlig-hellman |离散对数
1 | from Crypto.Util.number import * |
题解
- 昨天晚上集中学习了la佬的sage指南文章,恰好有离散对数问题(Pohlig-hellman)
- 唯一让我疑惑的是,la佬将n是合数、n是素数或素数的整数幂分为两类,其中n是素数里交代了Pohlig-hellman,但题目里n明显是后者🤔
虽然但是,sage一两行搞定
1 | # sage |
总结
离散对数的问题。
- 当模为素数时,一般用的是大步小步算法(BSGS)
- 当模为素数的幂时,主要用Pohlig-Hellman
而sage里的
discrete_log就是利用以上两种算法实现的???不确定有没有用Pohlig-Hellman算法,因为la佬说它要求底数是原根
想简单一点 |m=c
题目
1 | N = 24873777989291448485268365702265085243886872900039809831478881276969311714448924581398692832639705916538111455861057354225427758736198452679468399039512440497290615485190994957684665065261280544484301856860844163436499302230085760545686486398949018187416289923500558688885485672960734334858119391323987554701544773420070317895909846297195832399677291338220818181502181317849952785959097285626009703863257450199781708945715701136683994546852422993684382468187651935055302074609980311161155531603473091857526099148935429447319415714778860215376802270686310782735079899235228731429165106477537031235405221734008734614847 |
hint: 当你凝视密文的时候,密文也在凝视你
题解
糟了,菜🐔看着题目瑟瑟发抖🤔
c甚至没有e大, 想了很久没想到
最后看4XWi11师傅题解,直接把c转byte得解(半瞬间有过这个想法)
1 | WINNER WINNER CHICKEN DINNER! This is easy but quite troll man. One should NOT expect that the ciphertext is equal to plaintext in the real world. Flag is: ctfshow{xielunyan___KAI!}. By the way, what a stupid encryption exponent it is! |
m = c
离谱,当个脑洞吧。
站在出题者角度来看是极好的,对于解题者看来一般。
致敬我费的时间😭
ctfshow·单身杯·TooYoungRSA|选择明文攻击
题目
chall.py
1 | from nevergonnagiveyouup import n, e |
题解
学习参考la佬博客
显而易见,求出k即解
而求k,则需要n、e
我们可以随意传m,并且得到他的密文,典型的选择明文攻击
实现如下
1 | # SageMath |
总结
适用于不知n、e,可以自己发m且得到c的情况
原理分析
首先发2,即:m = 2,则可得到
$c_2 = 2^e \mod n$
其次,我们再发送$2^2$,即:m=4, 则可得到:
$c4= 4^e \mod n$
为探究好两者之间的关系,不妨设$2^e = a+bn$, 则有:
$c_2=2^e \mod n = a+bn \mod n = a$
$c_4=4^e \mod n = (2^2)^e = (2^e)^2 = (a+bn)^2 = a^2+2abn+b^2n^2 = a^2 \mod n $
也即:$c_4 = a^2 + kn$, 而此时,我们构造下c2, 即:
$(c_2)^2 \mod n = a^2 \mod n $, 则: $(c2)^2 = a^2+k’n$
此时,记$A = (c2)^2 - c4=(k-k’)n = k’’n$
得到上一步后,我们再接着往下发送🙂
再则,我们发送$2^3$,即:m=8,同理,则可以得到:
$B = (c2)^3-c_8=k’’’n$
好起来了!
我们用$gcd(A, B)$即得到n,而保险起见,不妨多来几个($2^4、2^5···$)一起求最大公因子
防污染
为了防止k值污染到了n(即防止gcd得到的是 一些小数 * n),我们对得到的n简单清洗一下(这里前提是n由两大素数p、q相乘)
代码
1 | # 自己按照题目要求编写server_encode() 函数 |
同态加密
1 | from Crypto.Util.number import getPrime as getprime ,long_to_bytes,bytes_to_long,inverse |
$c = (g^m \mod n^2)*(r^n \mod n^2)\mod n^2 = g^m * r^n \mod n^2$
给c、n、g
Paillier密码,于1999年由Pascal Paillier发明,是一种用于公钥加密的概率非对称算法。该算法具有加法同态的性质 ; 这意味着,仅给出公钥和m1、m2加密,可以计算出m1 + m2
模式1
- 大素数p、q满足$gcd(pq, (p-1)*(q-1)) = 1$
- $n=p\cdot q,λ = lcm(p-1, q-1) = \frac{(p-1)\cdot (q-1) }{ gcd(p-1,q-1)}$
- 选g, $0<g<n^2$
- $L(x) = \frac{x-1}{n}$
- $μ = (L(g^λ \pmod {n^2} ))^{-1} \pmod n$
- 公钥:(n, g)
- 私钥:(λ,μ)
模式2
在模式1的基础上,改写g,λ,μ
- $g=n+1$
- $λ = φ(n) = (p-1)\cdot (q-1)$
- $μ = φ(n)^{-1} \pmod n$
加密
明文m需要满足$0≤m<n$
选择随机 r,且满足$gcd(r,n)=1$
密文:$c=g^m⋅r^n(\mod n^2)$
解密
$m = ( L( c^λ \pmod {n^2} ) \cdot μ ) \pmod n$
题解
分解n,得到p、q
然后跟着解密步骤解就完事了
🤔但p的bit数好像根题目不符
1 | import gmpy2 |
总结
同态加密基于rsa的大素数分解难题,能得到p、q又有公钥就可解
