Harry's Blog

温故知新

0%

GoogleCTF2022·Crypto 复现

发表于 更新于   阅读次数： Valine：
本文字数： 23k 阅读时长 ≈ 21 分钟
复现

2022GoogleCTF·密码复现

前言

复现参考官方仓库

很遗憾，虽然很热血、满怀激情地熬夜打比赛

但被虐的体无完肤，48h队伍0解

「何时才能登陆梦中的彼岸」

FLAG

ELECTRIC MAYHEM CLS

题目

The server presents power traces of a secret firmware crypto operation. The goal is to recover the secret key. Note, the flag is ‘CTF{XXX}’ where XXX is your recovered key.

题解

学习参考密码魔女的wp

image-20220705180147886

真是糟糕，🧙‍♀️抄的别的师傅的分析代码（也是日本的师傅）

🧙‍♀️懂不懂原理我不知，但她确实没讲清楚

涉及“电力解析”，在我看来是很偏的知识点，不具备普适性，暂且搁置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
# ref: https://trmr.hatenablog.com/entry/2018/03/18/220441

import json
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio
from Crypto.Cipher import AES
import binascii
import sys

humming = [bin(n).count("1") for n in range(256)]

json_open = open('ELECTRIC MAYHEM CLS/stm32f0_aes.json', 'r')
json_load = json.load(json_open)

sbox = (
    0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
    0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
    0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
    0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
    0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
    0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
    0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
    0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
    0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
    0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
    0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
    0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
    0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
    0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
    0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
    0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16)


def addkey_subbytes(pt, guesskey):
    return sbox[pt ^ guesskey]


N = len(json_load)

print(N)
# print(json_load[0]['pt'])
# print(json_load[0]['ct'])
# print(json_load[0]['pm'])

bestguess = [0] * 16
data_start = 7
data_end = 200
NUM_POINTS = data_end - data_start
NUM_TRACES = len(json_load)
traces = []

for pt_ct_pm in json_load:
    traces.append(pt_ct_pm['pm'][data_start:data_end])

for k_idx in range(16):  # determine key index
    cpaoutput = [0] * 256

    # follow valiables may not be need
    maxcpa = [0] * 256
    bestcor = 0
    bestkey = 0

    for kguess in range(256):  # determine word key candidate
        sumnum = np.zeros(NUM_POINTS)
        sumden1 = np.zeros(NUM_POINTS)
        sumden2 = np.zeros(NUM_POINTS)

        hyp = np.zeros(NUM_TRACES)

        for t_idx in range(NUM_TRACES):  # hypothesis hamming weight
            hyp[t_idx] = humming[addkey_subbytes(json_load[t_idx]['pt'][k_idx], kguess)]

        h_mean = np.mean(hyp, dtype=np.float64)
        t_mean = np.mean(traces, axis=0, dtype=np.float64)

        assert 0 < h_mean and h_mean < 8, "meanh is not between 0 and 8"
        assert len(t_mean) == NUM_POINTS, "meant is less than trace points"

        cors = []

        for t_idx in range(NUM_TRACES):
            hdiff = (hyp[t_idx] - h_mean)
            tdiff = traces[t_idx] - t_mean

            sumnum = sumnum + (hdiff * tdiff)
            sumden1 = sumden1 + hdiff * hdiff
            sumden2 = sumden2 + tdiff * tdiff

        cpaoutput[kguess] = sumnum / np.sqrt(sumden1 * sumden2)

        maxcpa[kguess] = max(abs(cpaoutput[kguess]))

    bestguess[k_idx] = np.argmax(maxcpa)
    print("[+] best guess key [{0}] is {1:02x} (score: {2})".format(k_idx, bestguess[k_idx], maxcpa[bestguess[k_idx]]))

strkey = ''.join(map(chr, bestguess))
print(strkey)
# W0ckAwocKaWoCka1
# CTF{W0ckAwocKaWoCka1}

总结

不足

  • 搜索能力弱了，接受新鲜事物的能力也差

收获

  • 可以关注关注日韩CTF圈子

    不少密码难题的wp都是日韩出的，值得重视

CYCLING

题目

It is well known that any RSA encryption can be undone by just encrypting the ciphertext over and over again. If the RSA modulus has been chosen badly then the number of encryptions necessary to undo an encryption is small. However, if the modulus is well chosen then a cycle attack can take much longer. This property can be used for a timed release of a message. We have confirmed that it takes a whopping 2^1025-3 encryptions to decrypt the flag. Pack out your quantum computer and perform 2^1025-3 encryptions to solve this challenge. Good luck doing this in 48h.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#!/usr/bin/python3

# Copyright 2022 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
#      http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.

"""
It is well known that any RSA encryption can be undone by just encrypting the
ciphertext over and over again. If the RSA modulus has been chosen badly then
the number of encryptions necessary to undo an encryption is small.
If n = 0x112b00148621 then only 209 encryptions are necessary as the following
example demonstrates:

>>> e = 65537
>>> n = 0x112b00148621
>>> pt = 0xdeadbeef
>>> # Encryption
>>> ct = pow(pt, e, n)
>>> # Decryption via cycling:
>>> pt = ct
>>> for _ in range(209):
>>>   pt = pow(pt, e, n)
>>> # Assert decryption worked:
>>> assert ct == pow(pt, e, n)

However, if the modulus is well chosen then a cycle attack can take much longer.
This property can be used for a timed release of a message. We have confirmed
that it takes a whopping 2^1025-3 encryptions to decrypt the flag. Pack out
your quantum computer and perform 2^1025-3 encryptions to solve this
challenge. Good luck doing this in 48h.
"""

e = 65537
n = 0x99efa9177387907eb3f74dc09a4d7a93abf6ceb7ee102c689ecd0998975cede29f3ca951feb5adfb9282879cc666e22dcafc07d7f89d762b9ad5532042c79060cdb022703d790421a7f6a76a50cceb635ad1b5d78510adf8c6ff9645a1b179e965358e10fe3dd5f82744773360270b6fa62d972d196a810e152f1285e0b8b26f5d54991d0539a13e655d752bd71963f822affc7a03e946cea2c4ef65bf94706f20b79d672e64e8faac45172c4130bfeca9bef71ed8c0c9e2aa0a1d6d47239960f90ef25b337255bac9c452cb019a44115b0437726a9adef10a028f1e1263c97c14a1d7cd58a8994832e764ffbfcc05ec8ed3269bb0569278eea0550548b552b1
ct = 0x339be515121dab503106cd190897382149e032a76a1ca0eec74f2c8c74560b00dffc0ad65ee4df4f47b2c9810d93e8579517692268c821c6724946438a9744a2a95510d529f0e0195a2660abd057d3f6a59df3a1c9a116f76d53900e2a715dfe5525228e832c02fd07b8dac0d488cca269e0dbb74047cf7a5e64a06a443f7d580ee28c5d41d5ede3604825eba31985e96575df2bcc2fefd0c77f2033c04008be9746a0935338434c16d5a68d1338eabdcf0170ac19a27ec832bf0a353934570abd48b1fe31bc9a4bb99428d1fbab726b284aec27522efb9527ddce1106ba6a480c65f9332c5b2a3c727a2cca6d6951b09c7c28ed0474fdc6a945076524877680
# Decryption via cycling:
pt = ct
for _ in range(2**1025 - 3):
  print(_)
  pt = pow(pt, e, n)
  print(pt)
  if ct == pow(pt, e, n):
    break
# Assert decryption worked:

# Print flag:
print(pt.to_bytes((pt.bit_length() + 7)//8, 'big').decode())

题解

只有代码，没有解释原理的wp，看了半小时，看不懂😵‍💫

先放着吧（中文注释是我尝试理解所翻译的）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
import sympy, libnum
from math import gcd


# 常用字段大小的2**i-1的素因子表。这是必要的，因为该文件中的因式分解仅使用试用除法。


# 2^(L)-1就是二进制下L个1
# 以下数据来自: factor(2^(L)-1). 可用factor网页而不是sage
MERSENNE_PRIME_FACTORS = {
    64: [3, 5, 17, 257, 641, 65537, 6700417],
    96: [3, 3, 5, 7, 13, 17, 97, 193, 241, 257, 673, 65537, 22253377],
    128: [3, 5, 17, 257, 641, 65537, 274177, 6700417, 67280421310721],
    160: [
        3, 5, 5, 11, 17, 31, 41, 257, 61681, 65537, 414721, 4278255361,
        44479210368001
    ],
    192: [
        3, 3, 5, 7, 13, 17, 97, 193, 241, 257, 641, 673, 65537, 6700417,
        22253377, 18446744069414584321
    ],
    224: [
        3, 5, 17, 29, 43, 113, 127, 257, 449, 2689, 5153, 65537, 15790321,
        183076097, 54410972897, 358429848460993
    ],
    255: [
        7, 31, 103, 151, 2143, 11119, 106591, 131071, 949111,
        9520972806333758431, 5702451577639775545838643151
    ],
    256: [
        3, 5, 17, 257, 641, 65537, 274177, 6700417, 67280421310721,
        59649589127497217, 5704689200685129054721
    ],
    384: [
        3, 3, 5, 7, 13, 17, 97, 193, 241, 257, 641, 673, 769, 65537, 274177,
        6700417, 22253377, 67280421310721, 18446744069414584321,
        442499826945303593556473164314770689
    ],
    448: [
        3, 5, 17, 29, 43, 113, 127, 257, 449, 641, 2689, 5153, 65537, 6700417,
        15790321, 183076097, 54410972897, 358429848460993,
        167773885276849215533569, 37414057161322375957408148834323969],
    512: [
        3, 5, 17, 257, 641, 65537, 274177, 6700417, 67280421310721,
        1238926361552897, 59649589127497217, 5704689200685129054721,
        93461639715357977769163558199606896584051237541638188580280321
    ],
    768: [
        # factors of 2**384 - 1
        3, 3, 5, 7, 13, 17, 97, 193, 241, 257, 641, 673, 769, 65537, 274177,
        6700417, 22253377, 67280421310721, 18446744069414584321,
        442499826945303593556473164314770689,
        # factors of 2**128 + 1
        59649589127497217, 5704689200685129054721,
        # factors of 2**256 - 2**128 + 1
        349621839326921795694385454593,
        331192380488114152600457428497953408512758882817
    ],
    1024: [
        3, 5, 17, 257, 641, 65537, 274177, 6700417, 67280421310721,
        1238926361552897, 59649589127497217, 5704689200685129054721,
        93461639715357977769163558199606896584051237541638188580280321, 2424833,
        7455602825647884208337395736200454918783366342657,
        741640062627530801524787141901937474059940781097519023905821316144415759504705008092818711693940737
    ],
    2048: [
        3, 5, 17, 257, 641, 65537, 274177, 6700417, 67280421310721,
        1238926361552897, 59649589127497217, 5704689200685129054721,
        93461639715357977769163558199606896584051237541638188580280321, 2424833,
        7455602825647884208337395736200454918783366342657, 45592577, 6487031809,
        4659775785220018543264560743076778192897,
        741640062627530801524787141901937474059940781097519023905821316144415759504705008092818711693940737,
        130439874405488189727484768796509903946608530841611892186895295776832416251471863574140227977573104895898783928842923844831149032913798729088601617946094119449010595906710130531906171018354491609619193912488538116080712299672322806217820753127014424577
    ]
}

def prod(f: list[int]) -> int:
  """计算累积结果"""
  res = 1
  for p in f:
    res *= p
  return res

def divisors_from_factors(factors: list[int]) -> list[int]:
    """计算给定因子的整数的除数列表

    >>> divisors_from_factors([2,5])
    [1, 2, 5, 10]
    """
    res = {1}
    for f in factors:
      res |= set(x * f for x in res)
    return sorted(res)

class CycleLength:
  """Computes properties of RSA keys with a known cycle length.

  An instance of this class gives properties of RSA moduli n with
  the property that lambda(lambda(n)) divides max_cycle.
  The computation of these properties requires to know the factorization
  of max_cycle. Hence we use values for max_cycle for which the factorization
  is known. For example one can use max_cycle = 2 * (2^m - 1) and just
  look up the factorization of the Mersenne number 2^m - 1.

  This is code that is both used for generating challenges and for solving them.
  """

  def __init__(self, max_cycle_factors: list):
    """Defines the length of the cycle. 

    Args:
      max_cycle_factors: a list of prime factors of the maximal cycle
    """
    self.max_cycle_factors: list[int] = max_cycle_factors
    self.max_cycle = prod(max_cycle_factors)

    # A list of possible divisors of max_cycle
    self.max_cycle_divisors = divisors_from_factors(max_cycle_factors)

    # A list of primes with the property that r - 1 divides max_cycle.
    self.primes_ = None

  def primes(self) -> list:
    """Returns a list of primes r, such that r-1 divides self.max_cycle."""
    if self.primes_ is None:
      self.primes_ = [d + 1 for d in self.max_cycle_divisors
                      if sympy.isprime(d + 1)]
    return self.primes_

def solve(n: int, cycle_length: CycleLength, m0: int = 3, max_attempts: int = 10):
  print(m0, max_attempts)  # 3 10
  for m in range(m0, m0 + max_attempts):
    for p in cycle_length.primes():
      m = pow(m, p, n)
      g = gcd(m - 1, n)
      if 1 < g < n:
        return g, n//g

def solve_challenge(n, cycle_length):
  res = solve(n, cycle_length)
  if res:
    p, q = res
    if 1 < p < n and 1 < q < n and p*q == n:
      return p, q 
  return None

e = 65537
n = 0x99efa9177387907eb3f74dc09a4d7a93abf6ceb7ee102c689ecd0998975cede29f3ca951feb5adfb9282879cc666e22dcafc07d7f89d762b9ad5532042c79060cdb022703d790421a7f6a76a50cceb635ad1b5d78510adf8c6ff9645a1b179e965358e10fe3dd5f82744773360270b6fa62d972d196a810e152f1285e0b8b26f5d54991d0539a13e655d752bd71963f822affc7a03e946cea2c4ef65bf94706f20b79d672e64e8faac45172c4130bfeca9bef71ed8c0c9e2aa0a1d6d47239960f90ef25b337255bac9c452cb019a44115b0437726a9adef10a028f1e1263c97c14a1d7cd58a8994832e764ffbfcc05ec8ed3269bb0569278eea0550548b552b1
ct = 0x339be515121dab503106cd190897382149e032a76a1ca0eec74f2c8c74560b00dffc0ad65ee4df4f47b2c9810d93e8579517692268c821c6724946438a9744a2a95510d529f0e0195a2660abd057d3f6a59df3a1c9a116f76d53900e2a715dfe5525228e832c02fd07b8dac0d488cca269e0dbb74047cf7a5e64a06a443f7d580ee28c5d41d5ede3604825eba31985e96575df2bcc2fefd0c77f2033c04008be9746a0935338434c16d5a68d1338eabdcf0170ac19a27ec832bf0a353934570abd48b1fe31bc9a4bb99428d1fbab726b284aec27522efb9527ddce1106ba6a480c65f9332c5b2a3c727a2cca6d6951b09c7c28ed0474fdc6a945076524877680

m = 1024  # 2^1025 - 3 是1025比特位的数
cycle_length = CycleLength([2] + MERSENNE_PRIME_FACTORS[m])  # 所以补一个2
p, q = solve_challenge(n, cycle_length)
phi = (p-1)*(q-1)
d = pow(e, -1, phi)
pt = int(pow(ct, d, n))
print(libnum.n2s(pt))
# b'CTF{Recycling_Is_Great}'

xchgeaxeax师傅分享了他找到的wp，膜拜了下来自日本的密码魔女wp

不得不说，技术力拉满，但魔女🧙‍♀️表达能力太差了。

也或许是日语机翻的问题，看起来实在太差劲了，一题看一天…

来分析一下题目吧！

It is well known that any RSA encryption can be undone by just encrypting the ciphertext over and over again.

根据题意，“任何RSA加密都能被循环加密所解密”

其后，给了个例子

1
2
3
4
5
e = 65537
n = 0x112b00148621
pt = 0xdeadbeef
# Encryption
ct = pow(pt, e, n)

以上为对明文为deedbeef加密的过程

1
2
3
4
5
6
# Decryption via cycling:
pt = ct
for _ in range(209):
	pt = pow(pt, e, n)
print(str(hex(pt)).replace(r'0x', ''))
# deadbeef

可见，直接对密文加密209次就能得到明文

而根据这个性质，可以人为选好e、n控制好循环次数，达到定时公布消息的功能

之后，给了flag相关的e、n、ct，以及循环次数$2^{1025}-3$

循环次数过于大了，普通机子直接跑48h时间应该是不够的

需要更好的算法求解问题

聚焦循环加密的解密过程，有以下：

$m≡c^{e^{2^{1025}-3}}≡(m^e)^{e^{2^{1025}-3}}≡m^{e^{2^{1025}-2}} \mod n$

可得：

1⃣️$d≡e^{2^{1025}-3}$

2⃣️$ed≡e^{2^{1025}-2}≡1 \mod phi$

对1⃣️，因为d太大了，算不出来，就算我们有了私钥d也不能解出明文，若想着硬算出d同直接循环求解没本质区别

对2⃣️，由欧拉定理，可得：$\phi(phi) = 2^{1025-2}$，记为3⃣️

接下来的手法，我只能从解释的角度出发了，至于当时让我想，应该是想不出来的。

看到官方exp里，有专门的名字，或许是常用攻击方法？还得学习

为解决此题，我们需要找到一个相对够小的d，至少我们能算出来

如何减小d的大小又不影响解密呢？

答案是：$d \mod phi$

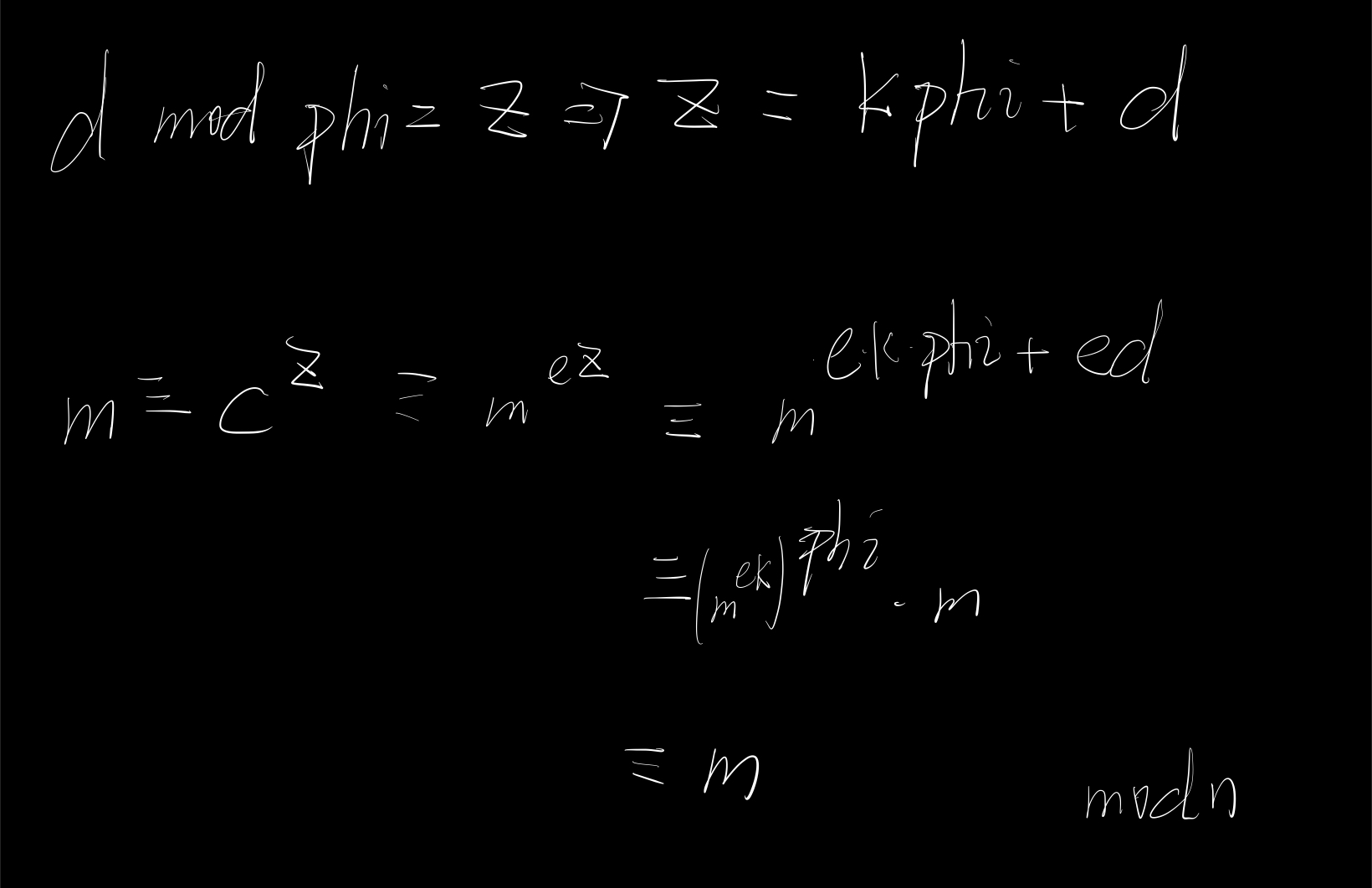
dmphi

其实，这是走不通的，因为我们不知道phi是多少，这样反而让未知量越来越多了

但，也不是没有收获，针对phi不知的问题，可以利用3⃣️，有：

$\phi(phi) = 2^{1025}-2$

拆之，得：

phi(phi)

而设$n=p*q$,则设：$phi=(p-1)•(q-1)=A•B•C•D•E•F•…$

又：$\phi(phi) = 2^{1025}-2=(A-1)•(B-1)•(C-1)•(D-1)•(E-1)•(F-1)•…$

$=a•b•c•d•e•f•g•h•…$

也就是说，$A-1$可能被拆成了$a•b$, $B-1$可能被拆成了$c•e•h$

所以，排列组合并相乘$\phi(phi)$的素因子，再+1，我们能得到含有phi的式子

$(a•b+1)(a•c+1)(a•d+1)···(a•b•c+1)···(c•e•h+1)···$

就会得到$K•A•B•C•D•E•F…=K*phi$

总之，利用$\phi(phi)$的素因子，我们能恢复出$K*phi$

实现代码，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
from Crypto.Util.number import *
import itertools
import math

lambda_lambda_divs = [
 2,
 3,
 5,
 17,
 257,
 641,
 65537,
 274177,
 2424833,
 6700417,
 67280421310721,
 1238926361552897,
 59649589127497217,
 5704689200685129054721,
 7455602825647884208337395736200454918783366342657,
 93461639715357977769163558199606896584051237541638188580280321,
 741640062627530801524787141901937474059940781097519023905821316144415759504705008092818711693940737
 ]

lambda_lambda = 1
for d in lambda_lambda_divs:
    lambda_lambda *= d

assert lambda_lambda == 2**1025-2

lambda_candidate = 1

for d in lambda_lambda_divs:
    lambda_candidate *= (d+1)**10

cand = lambda_lambda_divs[:5]

res = 1
cnt = 0
for L in range(0, len(lambda_lambda_divs) + 1):
    for subset in itertools.combinations(lambda_lambda_divs, L):
        print(f"{cnt}")
        cnt += 1
        a = 2*math.prod(subset)+1
        if isPrime(a):
            res *= a

再回到如何减小d的大小又不影响解密这个问题，不难发现：

可用$d \mod K*phi$

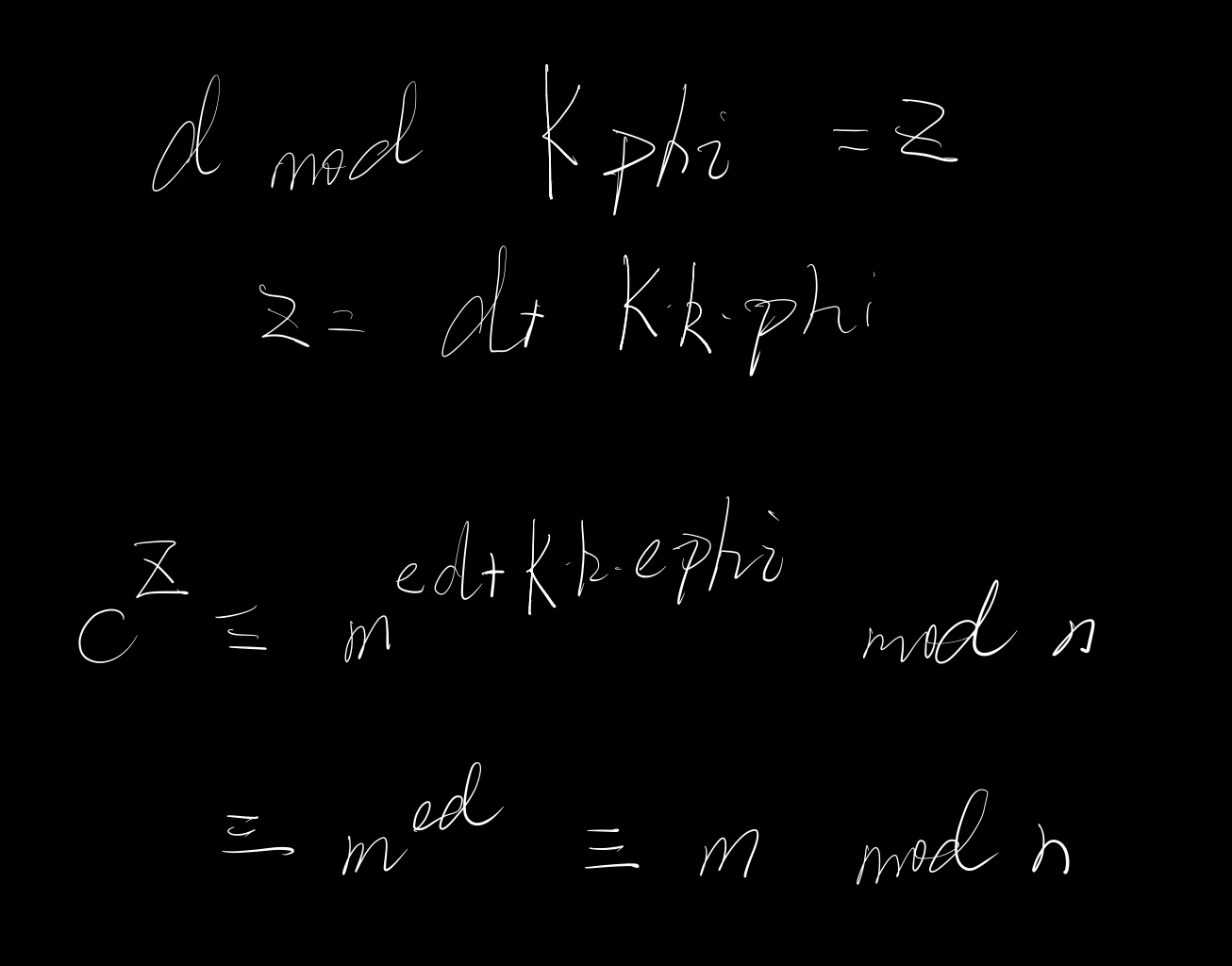
dmkphi

也即：可利用较小的$d \mod K*phi$（原来d为$e^{2^{1025}-3}$）来当私钥d，解密出明文m

（前面算得的K*phi记为res）

1
2
3
p = pow(e,2**1025-3,res)  # d mod K*phi
pt = pow(ct, p, n)
print(pt.to_bytes((pt.bit_length() + 7)//8, 'big').decode())

看到这p = pow(e,2**1025-3,res)，会发现这计算量也不小，能不能优化呢？

$e^{2^{1025}-3}≡e^{2^{1025}-2}•e^{-1}≡e^{-1} \mod K•phi$

（哪位师傅来教一下我，为什么可以）

1
2
3
p = pow(e,-1,res)  # d mod K*phi
pt = pow(ct, p, n)
print(pt.to_bytes((pt.bit_length() + 7)//8, 'big').decode())

总代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
from Crypto.Util.number import *
import itertools
import math

e = 65537
n = 0x99efa9177387907eb3f74dc09a4d7a93abf6ceb7ee102c689ecd0998975cede29f3ca951feb5adfb9282879cc666e22dcafc07d7f89d762b9ad5532042c79060cdb022703d790421a7f6a76a50cceb635ad1b5d78510adf8c6ff9645a1b179e965358e10fe3dd5f82744773360270b6fa62d972d196a810e152f1285e0b8b26f5d54991d0539a13e655d752bd71963f822affc7a03e946cea2c4ef65bf94706f20b79d672e64e8faac45172c4130bfeca9bef71ed8c0c9e2aa0a1d6d47239960f90ef25b337255bac9c452cb019a44115b0437726a9adef10a028f1e1263c97c14a1d7cd58a8994832e764ffbfcc05ec8ed3269bb0569278eea0550548b552b1
ct = 0x339be515121dab503106cd190897382149e032a76a1ca0eec74f2c8c74560b00dffc0ad65ee4df4f47b2c9810d93e8579517692268c821c6724946438a9744a2a95510d529f0e0195a2660abd057d3f6a59df3a1c9a116f76d53900e2a715dfe5525228e832c02fd07b8dac0d488cca269e0dbb74047cf7a5e64a06a443f7d580ee28c5d41d5ede3604825eba31985e96575df2bcc2fefd0c77f2033c04008be9746a0935338434c16d5a68d1338eabdcf0170ac19a27ec832bf0a353934570abd48b1fe31bc9a4bb99428d1fbab726b284aec27522efb9527ddce1106ba6a480c65f9332c5b2a3c727a2cca6d6951b09c7c28ed0474fdc6a945076524877680

lambda_lambda_divs = [
 2,
 3,
 5,
 17,
 257,
 641,
 65537,
 274177,
 2424833,
 6700417,
 67280421310721,
 1238926361552897,
 59649589127497217,
 5704689200685129054721,
 7455602825647884208337395736200454918783366342657,
 93461639715357977769163558199606896584051237541638188580280321,
 741640062627530801524787141901937474059940781097519023905821316144415759504705008092818711693940737
 ]

lambda_lambda = 1
for d in lambda_lambda_divs:
    lambda_lambda *= d

assert lambda_lambda == 2**1025-2

lambda_candidate = 1

for d in lambda_lambda_divs:
    lambda_candidate *= (d+1)**10

cand = lambda_lambda_divs[:5]

res = 1
cnt = 0
for L in range(0, len(lambda_lambda_divs) + 1):
    for subset in itertools.combinations(lambda_lambda_divs, L):
        print(f"{cnt}")
        cnt += 1
        a = 2*math.prod(subset)+1
        if isPrime(a):
            res *= a


p = pow(e,-1,res)
pt = pow(ct, p, n)
print(pt.to_bytes((pt.bit_length() + 7)//8, 'big').decode())
# CTF{Recycling_Is_Great}

总结

  • Cycle attack on RSA

    循环攻击给了确定次数，即可攻破

  • 通过$\phi(phi)$获得$K*phi$

  • d可以放缩成$d \mod K*phi$

MAYBE SOMEDAY

题目

Leave me your ciphertexts. I will talk to you later.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
#!/usr/bin/python3

# Copyright 2022 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
#      http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.

from Crypto.Util.number import getPrime as get_prime
import math
import random
import os
import hashlib

# Suppose gcd(p, q) = 1. Find x such that
#   1. 0 <= x < p * q, and
#   2. x = a (mod p), and
#   3. x = b (mod q).
def crt(a, b, p, q):
    return (a*pow(q, -1, p)*q + b*pow(p, -1, q)*p) % (p*q)

def L(x, n):
    return (x-1) // n

class Paillier:
    def __init__(self):
        p = get_prime(1024)
        q = get_prime(1024)

        n = p * q
        λ = (p-1) * (q-1) // math.gcd(p-1, q-1) # lcm(p-1, q-1)
        g = random.randint(0, n-1)
        µ = pow(L(pow(g, λ, n**2), n), -1, n)

        self.n = n
        self.λ = λ
        self.g = g
        self.µ = µ

        self.p = p
        self.q = q

    # https://www.rfc-editor.org/rfc/rfc3447#section-7.2.1
    def pad(self, m):
        padding_size = 2048//8 - 3 - len(m)
        
        if padding_size < 8:
            raise Exception('message too long')

        random_padding = b'\0' * padding_size
        while b'\0' in random_padding:
            random_padding = os.urandom(padding_size)

        return b'\x00\x02' + random_padding + b'\x00' + m

    def unpad(self, m):
        if m[:2] != b'\x00\x02':
            raise Exception('decryption error')

        random_padding, m = m[2:].split(b'\x00', 1)

        if len(random_padding) < 8:
            raise Exception('decryption error')

        return m

    def public_key(self):
        return (self.n, self.g)

    def secret_key(self):
        return (self.λ, self.µ)

    def encrypt(self, m):
        g = self.g
        n = self.n

        m = self.pad(m)
        m = int.from_bytes(m, 'big')

        r = random.randint(0, n-1)
        c = pow(g, m, n**2) * pow(r, n, n**2) % n**2

        return c

    def decrypt(self, c):
        λ = self.λ
        µ = self.µ
        n = self.n

        m = L(pow(c, λ, n**2), n) * µ % n
        m = m.to_bytes(2048//8, 'big')

        return self.unpad(m)

    def fast_decrypt(self, c):
        λ = self.λ
        µ = self.µ
        n = self.n
        p = self.p
        q = self.q

        rp = pow(c, λ, p**2)
        rq = pow(c, λ, q**2)
        r = crt(rp, rq, p**2, q**2)
        m = L(r, n) * µ % n
        m = m.to_bytes(2048//8, 'big')

        return self.unpad(m)

def challenge(p):
    secret = os.urandom(2)
    secret = hashlib.sha512(secret).hexdigest().encode()

    c0 = p.encrypt(secret)
    print(f'{c0 = }')

    # # The secret has 16 bits of entropy.
    # # Hence 16 oracle calls should be sufficient, isn't it?
    # for _ in range(16):
    #     c = int(input())
    #     try:
    #         p.decrypt(c)
    #         print('😀')
    #     except:
    #         print('😡')

    # I decided to make it non-interactive to make this harder.
    # Good news: I'll give you 25% more oracle calls to compensate, anyways.
    cs = [int(input()) for _ in range(20)]
    for c in cs:
        try:
            p.fast_decrypt(c)
            print('😀')
        except:
            print('😡')

    guess = input().encode()

    if guess != secret: raise Exception('incorrect guess!')

def main():
    with open('/flag.txt', 'r') as f:
      flag = f.read()

    p = Paillier()
    n, g = p.public_key()
    print(f'{n = }')
    print(f'{g = }')

    try:
        # Once is happenstance. Twice is coincidence...
        # Sixteen times is a recovery of the pseudorandom number generator.
        for _ in range(16):
            challenge(p)
            print('💡')
        print(f'🏁 {flag}')
    except:
        print('👋')

if __name__ == '__main__':
    main()

题解

学习参考xchgeaxeax师傅找到的日语wp

关于同态的选择密文攻击，时间不够，复现的话，下次一定！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
from ptrlib import Socket
from Crypto.Util.number import inverse
from itertools import product
import hashlib

table = []
for b in product(list(range(256)), repeat=2):
    table.append(hashlib.sha512(bytes(b)).hexdigest())

size = 10
basenum = int("3000" * size, 16)
basealp = int("6100" * size, 16)
one = int("0100" * size, 16)

sock = Socket("nc maybe-someday.2022.ctfcompetition.com 1337")

n = int(sock.recvlineafter("n = "))
g = int(sock.recvlineafter("g = "))

for stage in range(16):
    print("stage: {}".format(stage + 1))
    c0 = int(sock.recvlineafter("c0 = "))

    c1 = c0 * pow(g, 0xff << 1024, n ** 2) % (n ** 2)

    cs = []
    for i in range(20):
        if i <= 9:
            cs.append(c1 * inverse(pow(g, (basenum + one * i) << (1024 - size * 8 * 2), n ** 2), n ** 2) % (n ** 2))
        elif i <= 0xf:
            cs.append(
                c1 * inverse(pow(g, (basealp + one * (i - 10)) << (1024 - size * 8 * 2), n ** 2), n ** 2) % (n ** 2))
        else:
            cs.append(c1 * inverse(pow(g, (basenum + one * (i - 16)) << (1024 - size * 8 * 2 - 8), n ** 2), n ** 2) % (
                        n ** 2))

    for c in cs:
        sock.sendline(str(c))

    isin = [0 for _ in range(20)]
    for i, c in enumerate(cs):
        if '😀' in sock.recvline().decode():
            isin[i] = 1

    for h in table:
        head = h[:2 * size][::2]
        head2 = h[:2 * size + 1][1::2]
        match = True
        for i in range(16):
            if isin[i] == 1:
                if hex(i)[2:] not in head:
                    match = False
                    break
            else:
                if hex(i)[2:] in head:
                    match = False
                    break

        for i in range(4):
            if isin[i + 0x10] == 1:
                if hex(i)[2:] not in head2:
                    match = False
                    break
            else:
                if hex(i)[2:] in head2:
                    match = False
                    break

        if match:
            sock.sendline(h)
            line = sock.recvline().decode()
            if '💡' in line:
                break
            else:
                print(line)
                raise ValueError("bad luck")
    else:
        raise ValueError("not found")

sock.interactive()
# CTF{p4dd1n9_or4cl3_w1th_h0mom0rph1c_pr0p3r7y_c0m6in3d_in7o_a_w31rd_m47h_puzz1e}