初赛
电台签到
题目给了明文、密钥本,需要算出密文且发送出去
根据微信里公众号提示,找到密码本,进行模10运算,得到:

也根据微信里提示,先用BurpSuit抓包发s,然后修改再发上面的数字,即:
GET /send?msg=sJ HTTP/1.1GET /send?msg=2975115315066710252297245914J HTTP/1.1
ISO-9798-2(未解)
没有源码文件
1 | b'sha256(XXXX+tbEA66kfcvrpWVf7) == ffde1acf2b63699d40134576ad264b709da89e02cfdc8558e57ff3f24fc36fc5\n' |
其他
基础挑战码的可信计算1、2、3
非预期
- linux关键词查找
flag - root密码toor,重复以上
预期
太菜了,没预期出来
赛后没环境、没文件,没法复现
区块链
实验室区块链方向的师傅出了,最近打算入个门😈
初赛总结
密码出的太❌了,好像啥都有,但正儿八经的、含有数学原理的代码没看到一行👿
实话实说,给我整emo了😭
东北赛区复赛
gcrd2(100)
题目
1 | import numpy as np |
题解
1 | aT = np.dot(a, T) |
可知:T为矩阵aT、bT的最大右公因子

由gcrd得:
将aT、bT堆叠成$\begin{bmatrix} aT \\ bT\end{bmatrix}$,初等行变化 将下端化为0(我理解就是行阶梯形矩阵)
又仔细看a*T 与 b*T,发现每个数居然也都小于10
可想而知,T应该是极为稀疏的矩阵,最后用matlab的rref()函数,得到单位矩阵,应证猜想
1 | aTbT = [8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8; |
舍去下半部分0矩阵,得到32*32的单位阵T
代回题目,得解
1 | import hashlib |
math1(200)
题目
1 | import gmpy2 |
题解
$n_1 = a_1b_1+1,n_2=a_2b_2+1, n_3 = a_1b_2+1,v_2=kb_1+1$,且都为素数
$\phi _{n{_1}} = (n_1-1)(n_2-1) = a_1a_2b_1b_2=v_1$
$\phi _{n{_2}} = (n_3-1)(v_2-1) = a_1b_2kb_1$
由k=(a3*inverse(a3,v1)-1)//v1 、e=a3知:
$k = \frac{e • dinv(e, \phi_{n_1}) -1}{phi} = \frac{ed-1}{\phi_{n_1}} = \frac{k • \phi_{n_1}}{ \phi_{n_1}} = k$
解题思路也是明确的,知道e了,只要知道一个phi就可以求出对应私钥d,便可求解明文m
试了许多方式,题目说数学很重要,以为是n1间n2相乘后有什么关系,但形式越发复杂,无果
加减乘都无效后,尝试除,起初也没看到直接的破题点
后看着题目math1,猛然想起除法所对应连分数,试着分析了下
$\frac{N2}{N1}=\frac{(a_1b_2+1)(kb_1+1)}{(a_1b_1+1)(a_2b_2+1)}≈\frac{a_1b_2kb_1}{a_1b_1a_2b_2}=\frac{k}{a_2}$

再根据Legendre理论,$\frac{k}{a_2}$为$\frac{N2}{N1}$连分数
便可求出一系列的k、a2可能值
又有 $ed-1=k \phi_{n_1}$,所以:
$$\phi_{n_1} ≡ (-1)*k^{-1} \mod e$$
以及
$$\phi_{n_1} ≡ a_1a_2b_1b_2 = 0 \mod a_2$$
利用中国剩余定理联立之,得到$\phi_{n_1} \mod ea_2$
最后,为进一步确定确定$\phi_{n_1}$值,利用:$|𝜙−N1|=|(n_1−1)(n_2−1)−n_1n_2|=|-n_1−n_2+1|≈n_1+n_2 ≤ 2^{513}$
1 | import gmpy2 |
总而言之 我们用中国剩余定理得到了$\phi(n_1)$,而他不是真正的$\phi(n_1)$,,可以理解为真正的$phi(n_1) \mod e*a2$的余数
我们需要扩大它 即:$\phi(n_1) = crt结果+k•e•a2$
但$e•a2$才512bit ,简单估计一下,$\phi(n_1)$与n1相近,应该是1024bit左右
如果直接从crt结果开始 从k=1开始遍历 太慢了!
需要适当的「放缩」来选择合适的范围来遍历,以加速,$\phi(n_1)$与N1相近, 就本能的往N1上靠近
于是有 phi1 = phi_ + (N1 // bound) * bound
但显然 phi1的初始值(还没开始遍历k扩大) 是有可能大于N1的,就得缩小
这里可以大致估计的 按照期望 a1b1 、a2b2、ea2大小应该差不多,差了 a1b1 + a2b2 差不多就差了$2•e•a2$即$2•bound$
但前面加了 phi_ 保险起见应该再减多一个$e•a2$,经调试,的确如此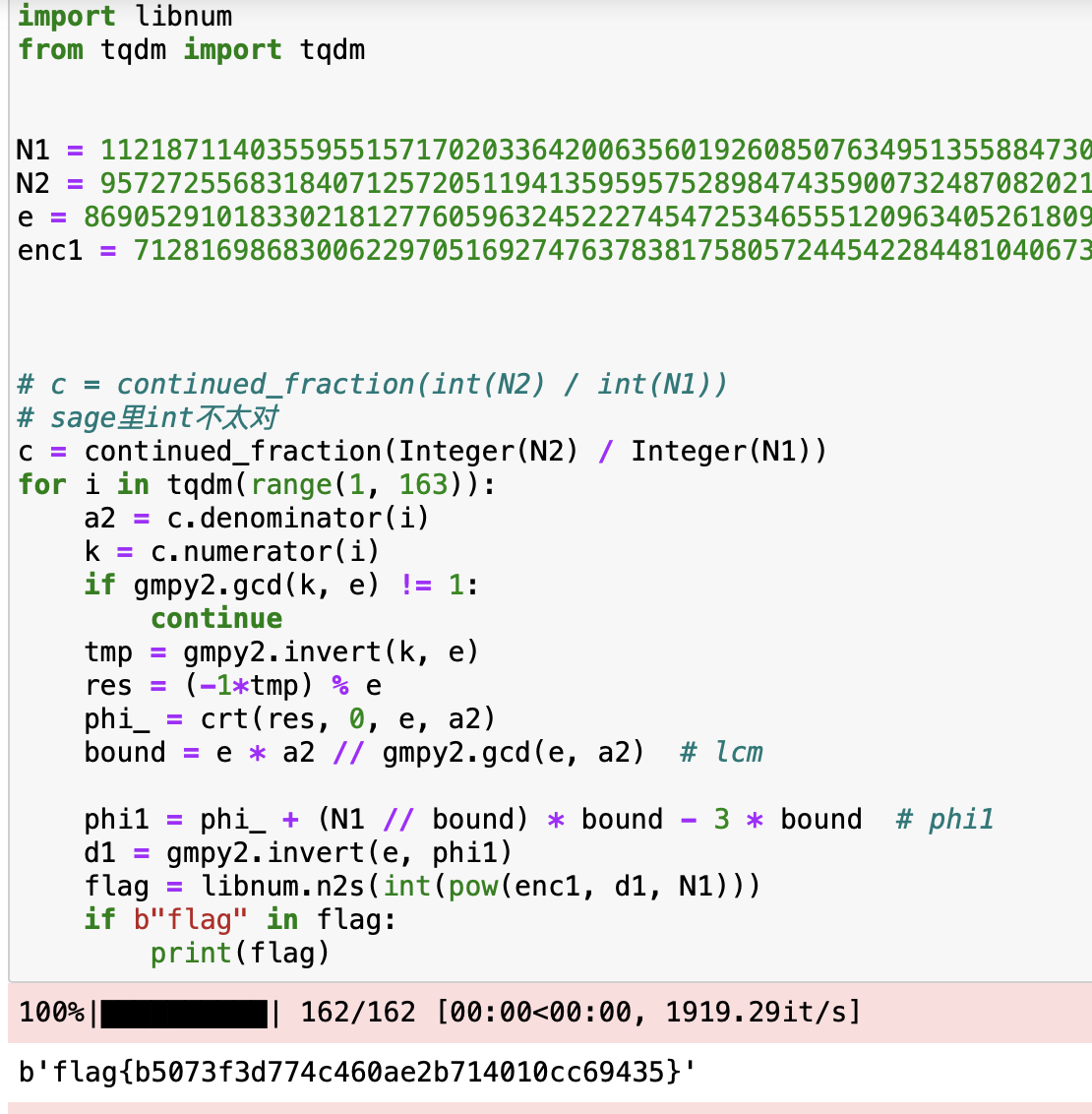
Rand0m3(200)
题目
1 | #!/usr/bin/python3 |
题解
巧,上个月刷到原题了,当时没写出来
赛后跟着wp尝试复现了下,居然撞上了
察觉后,觉得略有不同,在交互上卡了好一会,最后发现确实是一致的
想清楚了,思路也清晰
首先,关注题目中的加密代码
1 | def encrypt(s, k): |
破题点在于% 0xff,这样导致第一步的enc范围固定下来,只能是0到254
其后,enc = ord(c) ^ enc,那么ord(c)就不可能与0b11111111(255)异或
所以为确定一位flag字符,只要进行多次encrypt,在0到255中排除到只剩1个数,那么它就是flag[i]^255(key不妨就设为255)的结果
那么,都确定好后,根据异或可逆性质再异或回来即可
1 | from pwn import * |
fcsr (未解)
task.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79from random import getrandbits
bits = 80
mask = 2 ** bits - 1
feedback = 0xae985dff26619fc58623dc8aaf46d5903dd4254e # ???
class Task:
def __init__(self, key, iv):
self.key = key
self.iv = iv
self.filter = feedback
self.state = (self.iv << bits) | self.key # 或运算
self.C = 0
S = [0] * 20 # [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for i in range(20):
self.clock()
S[i] = self.F()
self.state = 0
for i in range(20):
shift = i * 8
self.state |= (S[i] << shift)
self.C = 0
for _ in range(162):
self.clock()
def clock(self):
tmp = self.state & 1
if tmp:
fb = feedback
else:
fb = 0
self.state = self.state >> 1
buffer = self.state ^ self.C
self.C &= self.state
self.C ^= (buffer & fb)
buffer ^= fb
self.state = buffer
def F(self):
buffer = self.filter & self.state
buffer ^= ((buffer >> 32) & 0xffffffff)
buffer ^= ((buffer >> 64) & 0xffffffff)
buffer ^= ((buffer >> 96) & 0xffffffff)
buffer ^= ((buffer >> 128) & 0xffffffff)
buffer = buffer & 0xffffffff
buffer ^= (buffer >> 16)
buffer ^= (buffer >> 8)
return buffer & 0xff
def encrypt(self, msg):
length = len(msg)
res = b""
for i in range(length):
self.clock()
res += bytes([self.F() ^ msg[i]])
return res
key = getrandbits(bits)
iv = getrandbits(bits)
print(key)
print(iv)
ffcsr = Task(key, iv)
f = open("hint", "wb")
for i in range(2 ** 26):
ffcsr.clock()
f.write((ffcsr.F().to_bytes(1, "big")))
f.close()
flag = b"flag{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}"
f = open("flag", "wb")
enc = ffcsr.encrypt(flag)
f.write(enc)
f.close()flag
hint
总结
还有一道fcsr(400分,0解)没出也没细研究
虽然时间上确实有些来不及了,但本质上还是怠惰了、畏难了
要是别的师傅一看赛题,东北赛区的密码师傅就这?
可太丢脸了😢