LFSR
即线性反馈移位寄存器,一个LFSR由若干个时钟存储元件(触发器)和一个反馈路径组成。
几个概念
LFSR作用
产生长伪随机序列,通常为二进制
存储元件(触发器)
存储数据的一个概念,知道可以存数据即可。
反馈路径
计算移位寄存器中某些触发器的XOR和,并将其传递。
度
LFSR由若干时钟存储元件(触发器)组成,而存储元件的个数就是LFSR的度。
简单LFSR
考虑度m=3、拥有三个触发器的FF2、FF1和FF0,且反馈路径如下
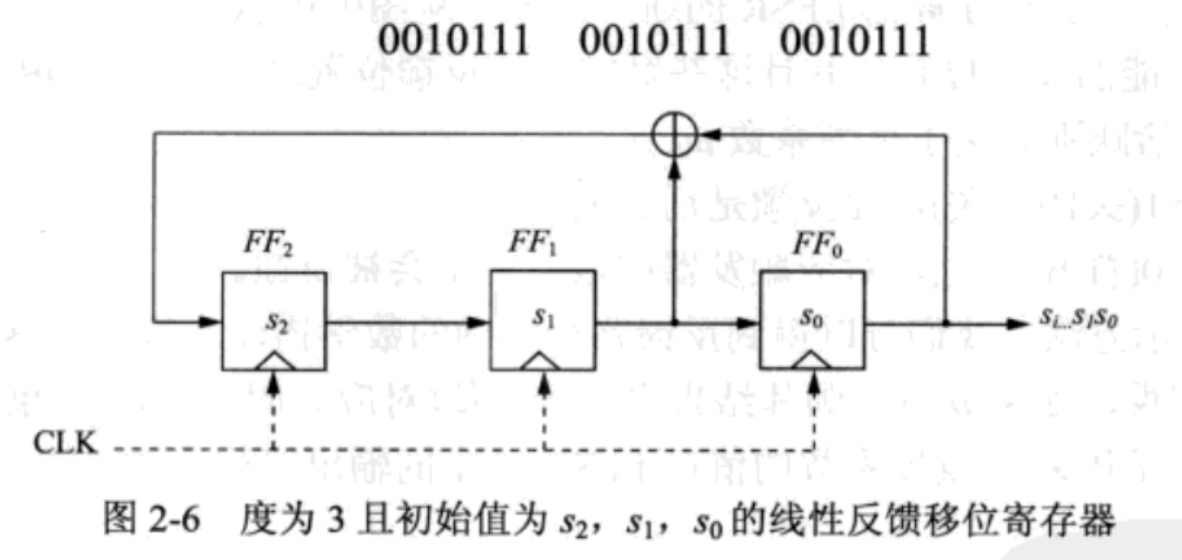
让我们来看看它究竟是如何运作的,又有什么性质。
假设初始状态为:S2=1, S1=0, S0=0 ;最右位的FF0往外输出
在每一个时间单位下,内部状态位向右移动一位
从左往右看
- 原先S2的值(1)给到 FF1
- 原先S1的值(0)给到 FF0
- 原先S0的值(0)和 原先S1的值(0)异或后(得到0)给到 FF2
- 原先S0的值(0)输出,LFSR得到数据 0
多次移位后,得到数据
Clk FF2 FF1 FF0=si 0 1 0 0 1 0 1 0 2 1 0 1 3 1 1 0 4 1 1 1 5 0 1 1 6 0 0 1 7 1 0 0 8 0 1 0
可见,LFSR从第6个时间周期后开始重复,这意味此LFSR周期长度为7
接下来,我们试着用一个简单的公式来描述此过程。
$$ S3 ≡ S1 + S0 \mod 2$$
$$ S4 ≡ S2 + S1 \mod 2$$
$$ S5 ≡ S3 + S2 \mod 2$$
$$ …$$
其中 Si 就是第i次输出的数据,i从0开始
而这里的S3其实就是第2步中FF2获得的值,右移了几次所输出的
不难归纳出输出位的计算公式为:
$$ S_{i+3} ≡ S_{i+1} + S_i \mod 2$$
其中,i = 0, 1, 2…
通过以上这个简单例子,我们便知晓了LFSR的大致流程与具有周期这个性质。
接下来,向现实迈进!
LFSR通用形式
考虑一个度为m的LFSR通用形式。
还得再提一个概念
反馈系数
某条反馈路径是否活跃取决于反馈系数P0, P1, …, Pm-1
- 若Pi = 1,此反馈是活跃的
- 若Pi = 0,对应触发器的输出将不会被反馈
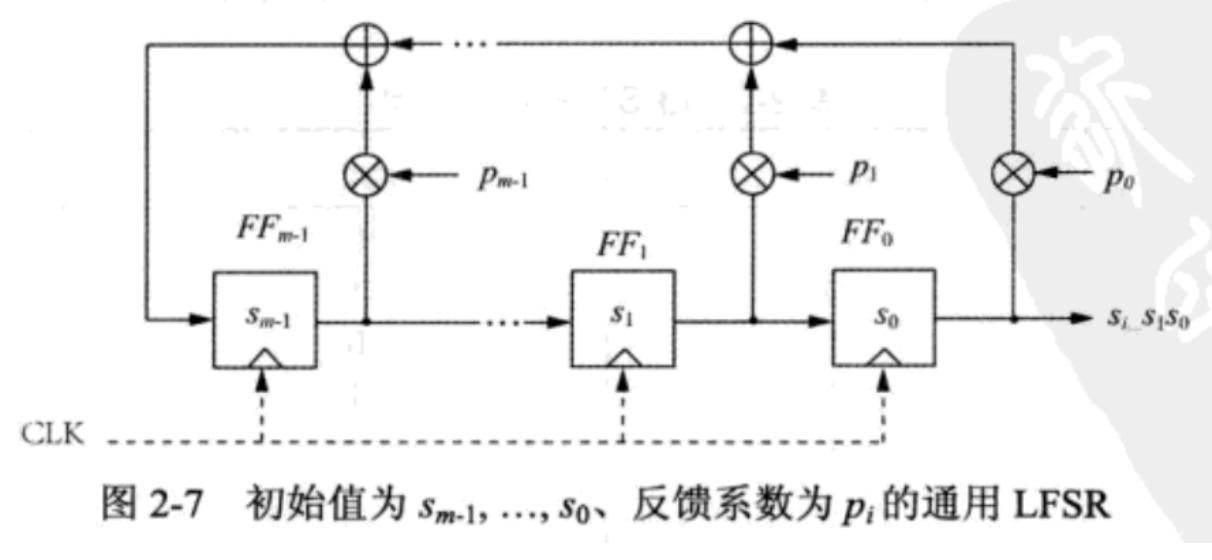
反馈系数很好理解。
在简单LFSR只异或、移位的基础上,多乘一个系数P罢了。
例如,对于 Sm-1 在一个周期内
- 它的值给到下一个触发器
- 还有条支路,导致 Sm-1 需要去乘 Pm-1,再异或
此时可见,若Pm-1 = 0,乘后得到的结果就是0,0再去与其他值异或,对异或的结果不造成影响。
接下来我们再对其具体性质进行剖析。
假设这个LFSR初始加载的值为S0, …, Sm-1, 则LFSR的下一个输出位Sm,可表示为:
$$S_m ≡ S_{m-1}P_{m-1} +···+ S_1P_1 + S_0P_0 \mod 2$$
再下一个输出位:
$$S_{m+1} ≡ S_{m}P_{m-1} +···+ S_2P_1 + S_1P_0 \mod 2$$
归纳,可得:
$$S_{i+m} ≡ \sum_{j=0}^{m-1} P_{j}·S_{i+j} \mod 2; S_i, P_j∈{0, 1}; i = 0, 1, 2, …$$
为什么下一位输出是Sm,可以试着理解下
接下来介绍的概念,虽未见其作用,但终究决定拓展开来。
在简单LFSR的例子中,我们知道了周期性
问:度为m的LFSR可以产生 最大的 不重复序列长度是多少?
答案是显而易见的
度为m的LFSR可以产生的最大序列长度为$ 2^m-1 $
一言以蔽之
LFSR的输出由m个内部寄存器状态唯一确定
给定某个状态,也能确定下一个状态
所以,只要LFSR 回到 从前有过的任何一个状态,它将立即开始重复。
因此,问最大序列长度 就是 问最小正周期 也相当于 问m个寄存器能有多少个非零状态,自然是$ 2^m-1 $
注:必须排除所有为零的状态。若某LFSR状态为全零,输出值将一直为0,谈周期性没意义。
本原多项式
LFSR还可以用多项式表达:
$$ P(x)=x^m+P_{m-1}x^{m-1}+…+P_1x+P_0 $$
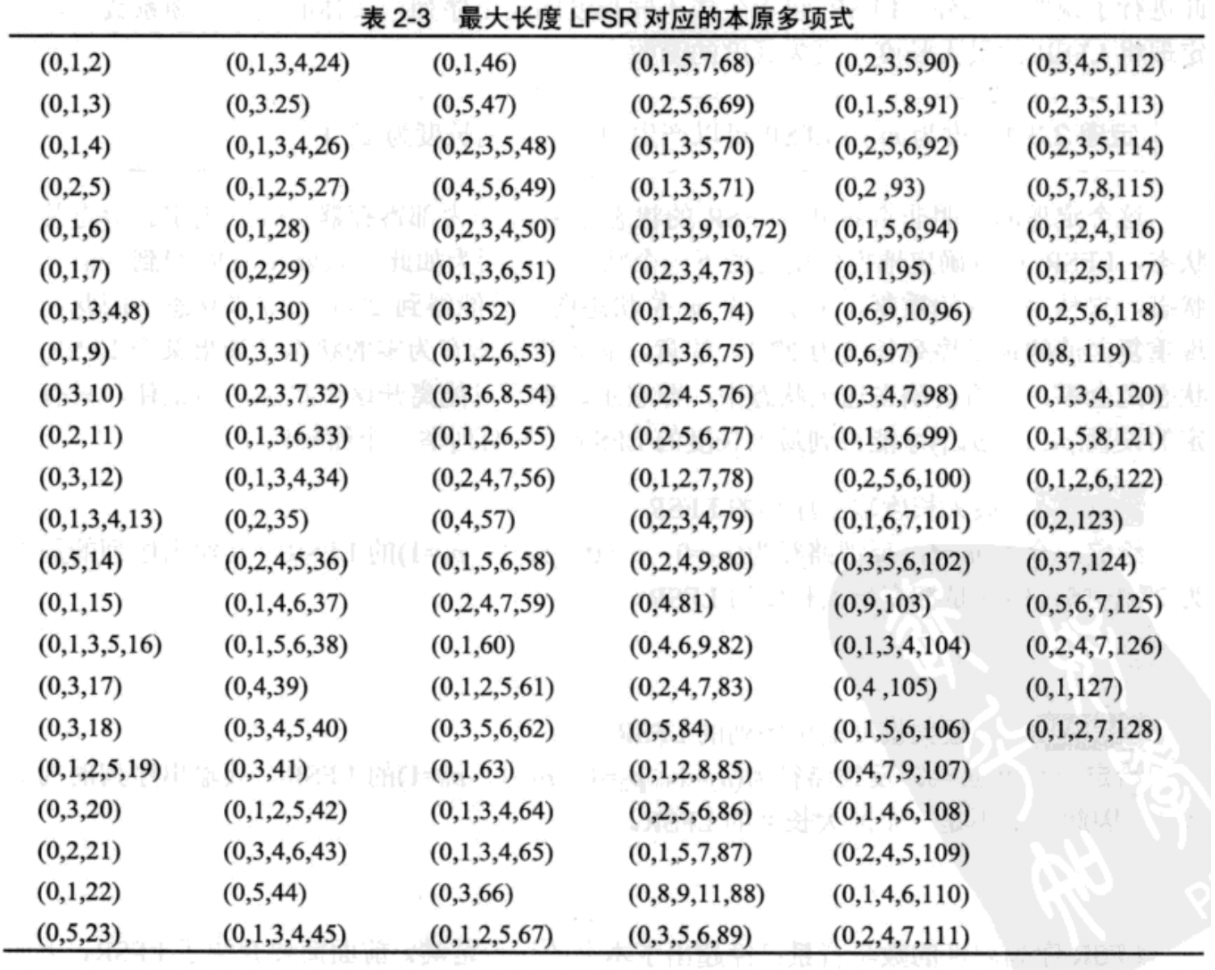
最大长度LFSR(周期为$ 2^m-1 $)拥有所谓的本原多项式
本原多项式是一种特殊的不可约分多项式,因子除了1就是多项式本身,此特性便利计算。
而对于同一个度m,可能存在多个本原多项式。
可见表格,其中(0, 1, 2)表示$1+ x + x^2$ ; (0, 2, 5)表示$ 1 + x^2 + x^5 $
那么,再对照多项式表达,便可知道对应反馈系数P的取值。
LFSR · 已知明文攻击
如果将LFSR当作序列密码使用,密钥K就是反馈系数向量(Pm-1, …, P1, P0)
若知道某些明文与对应的密文,便可发起攻击。
这里假设已经知道度m(不知道的话,可以一个个值爆破出来
理一下已知参数
度: m
已知明文: x0, x1, …, x2m-1
对应密文: y0, y1, …, y2m-1
第一步,异或得到2m个密钥序列位
$$ S_i ≡ x_i + y_i \mod 2; i=0, 1, …, 2m-1 $$
第二步,找出反馈系数Pi(密钥)
依据先前讨论,有 S 与 P 关系如下:
$$S_{i+m} ≡ \sum_{j=0}^{m-1} P_{j}·S_{i+j} \mod 2; S_i, P_j∈{0, 1}; i = 0, 1, 2, …$$
所以,得到:
$$ i=0, S_m ≡ P_{m-1}S_{m-1}+…+P_1S_1+P_0S_0 \mod 2$$
$$ i=0, S_{m+1} ≡ P_{m-1}S_{m}+…+P_1S_2+P_0S_1 \mod 2$$
$$ … $$
$$ i=m-1, S_{2m-1} ≡ P_{m-1}S_{2m-2}+…+P_1S_m+P_0S_{m-1} \mod 2$$
现在,咱有了m个未知数(P0, P1, …, Pm-1)的m个线性等式
可利用高斯消去、矩阵求逆等方法来解此线性等式系统
思路通而题可做矣