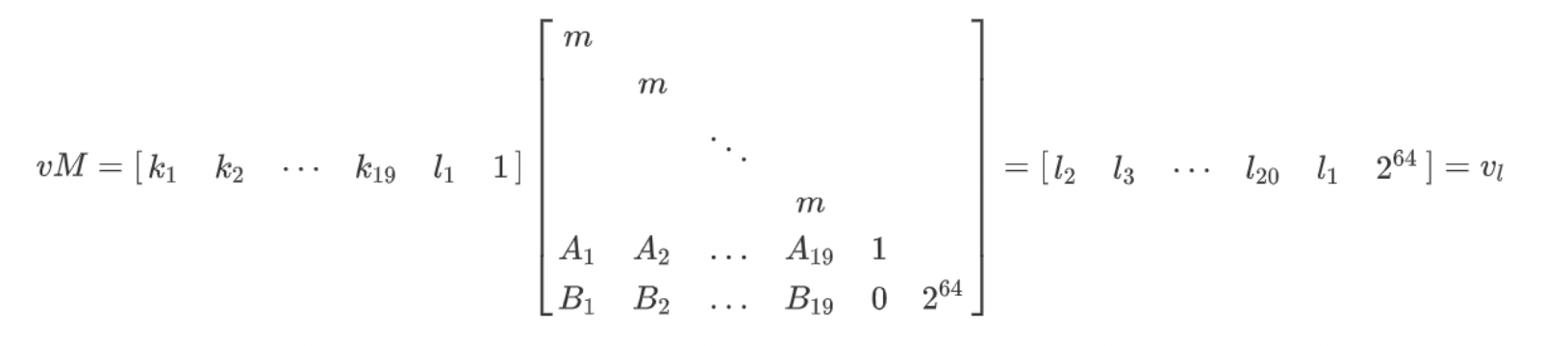格密码应用

NPUCTF2020[BABYLCG]

题目

from Crypto.Util.number import *
from Crypto.Cipher import AES
from secret import flag
class LCG:
    def __init__(self, bit_length):
        m = getPrime(bit_length)
        a = getRandomRange(2, m)
        b = getRandomRange(2, m)
        seed = getRandomRange(2, m)
        self._key = {'a':a, 'b':b, 'm':m}
        self._state = seed 
    def next(self):
        self._state = (self._key['a'] * self._state + self._key['b']) % self._key['m']
        return self._state
    def export_key(self):
        return self._key
def gen_lcg():
    rand_iter = LCG(128)
    key = rand_iter.export_key()
    f = open("key", "w")
    f.write(str(key))
    return rand_iter
def leak_data(rand_iter):
    f = open("old", "w")
    for i in range(20):
        f.write(str(rand_iter.next() >> 64) + "\n")
    return rand_iter
def encrypt(rand_iter):
    f = open("ct", "wb")
    key = rand_iter.next() >> 64
    key = (key << 64) + (rand_iter.next() >> 64)
    key = long_to_bytes(key).ljust(16, b'\x00')
    iv = long_to_bytes(rand_iter.next()).ljust(16, b'\x00')
    cipher = AES.new(key, AES.MODE_CBC, iv)
    pt = flag + (16 - len(flag) % 16) * chr(16 - len(flag) % 16)
    ct = cipher.encrypt(pt.encode())
    f.write(ct)
def main():
    rand_iter = gen_lcg()
    rand_iter = leak_data(rand_iter)
    encrypt(rand_iter)

if __name__ == "__main__":
    main()
"""
#key
{'b': 153582801876235638173762045261195852087, 'a': 107763262682494809191803026213015101802, 'm': 226649634126248141841388712969771891297}

#old
7800489346663478448
11267068470666042741
5820429484185778982
6151953690371151688
548598048162918265
1586400863715808041
7464677042285115264
4702115170280353188
5123967912274624410
8517471683845309964
2106353633794059980
11042210261466318284
4280340333946566776
6859855443227901284
3149000387344084971
7055653494757088867
5378774397517873605
8265548624197463024
2898083382910841577
4927088585601943730


#ct十六进制显示
00000000h: E0 E0 70 2C B7 D6 FC 19 AC E7 29 BE FC A4 0A F5 ; ààp,·Öü.¬ç)¾ü¤.õ
00000010h: 01 23 F7 A6 ED E1 F3 AE 4B 3A 2A CD 7B 1D D8 37 ; .#÷¦íáó®K:*Í{.Ø7
00000020h: 14 73 10 58 86 AF D1 57 73 44 1F A0 6C 65 6A D6 ; .s.X.¯ÑWsD..lejÖ
"""

题解

复现此题的契机是学习huangx师傅格密码中相关内容[1] 时所撞见，就此记录.

读题后，知题目给出了LCG中$a、b、m$与20次迭代过程中每次结果的高位，然后取第21次结果高位与第22次结果低64位组成key，第23次结果组成了iv，且给出了AES加密后密文.

不难想到，要求解此题，只需恢复出任意一次迭代结果。换句话说，就是需要求出至少一组的低64位数据，就能恢复出所有数据了.

设低位为$d_i$, 给出的高位数据记为$s_i=s_i<<64$

为解决这个问题，我们看向如下迭代过程:
$$
\begin{aligned} s_1+d_1 &= a•seed+b \mod m \\ s_2+d_2 &= a•(s_1+d_1)+b \mod m \\ &\vdots \\ s_n+d_n&=a•(s_{n-1}+d_{n-1})+b \mod m\end{aligned}
$$
有：
$$
\begin{aligned} s_2 + d_2 &= a(s_1+d_1)+b -km \\ d_2 &= as_1+b-s_2 +ad_1-km \\ 记 C&=as_1+b-s_2 \\ d_2 &= ad_1-km+C\end{aligned}
$$
这里将杂七杂八的已知量总和一起记为C，是极有意义的.

一来帮助化简，使得式子简洁明了；二来，为之后构造格打下基础，避免格中元素过多，维度过高.

回到题目里，上式中，未知量仅为$d_2、d_1、k$.

而构造格子，依据的准则可以是$\vec v •M=\vec w$，其中把已知量都放入M中，未知量放到$\vec v$中，要求量放在$\vec w$中。若构造合理，在对M运行LLL算法后，就能得到$\vec w$.

$d_2$可以用$d_1$表达，根据下式:
$$
\begin{aligned} d_1 &= d_1•1\\ d_2 &=ad_1-km+C \end{aligned}
$$
有如下构造
$$
\left(\begin {array}{c} d_1& -k & 1 \end{array} \right)
\left(\begin {array}{c} 1 & a & x_1\newline 0 & m & x_2 \newline 0 & C & x_3 \end{array} \right)
=\left(\begin {array}{c} d_1& d_2 & ? \end{array} \right)
$$
对构造细节，有如下：

• 为什么能确定M是3x3？

  $d_2$表达式中a、m、C的存在，导致要表达出$d_2$至少需要3个位置

• x能随便填吗？

  不能，由MINKOWSKI THEOREM，我们知道最短向量需满足$\lambda_1(Λ) \leq \sqrt{n} • \sqrt[n]{det(Λ)}$

  若格的行列式值较小，LLL所得结果就可能不是我们所预期的$\vec w$了

  由对角线法，可得$det(Λ)=mx_3-Cx_2$

  而为了让结果能校验且让最后一个数字尽可能地简单，$x_1、x_2$最好为0，结果则能固定为$x_3$,即:
  $$
  \left(\begin {array}{c} d_1& -k & 1 \end{array} \right)
  \left(\begin {array}{c} 1 & a & 0\newline 0 & m & 0 \newline 0 & C & x_3 \end{array} \right)
  =\left(\begin {array}{c} d_1& d_2 & x_3 \end{array} \right)
  $$

可得$det(Λ)=mx_3$，让$x_3$尽可能取大些，会相比让$x_3$取小更有可能LLL出$\vec w$

代码如下:

import gmpy2,libnum
from Crypto.Util.number import *

def next(s):
    return (a*s+b)%m

#key
a=107763262682494809191803026213015101802
b=153582801876235638173762045261195852087
m=226649634126248141841388712969771891297



s1 = 7800489346663478448 << 64
s2 = 11267068470666042741 << 64

C = a*s1+b-s2
print("C =", C)


x3 = 9999999999999999999999

M = matrix([[1, a, 0], [0, m, 0], [0, C, x3]])
print(M.LLL())

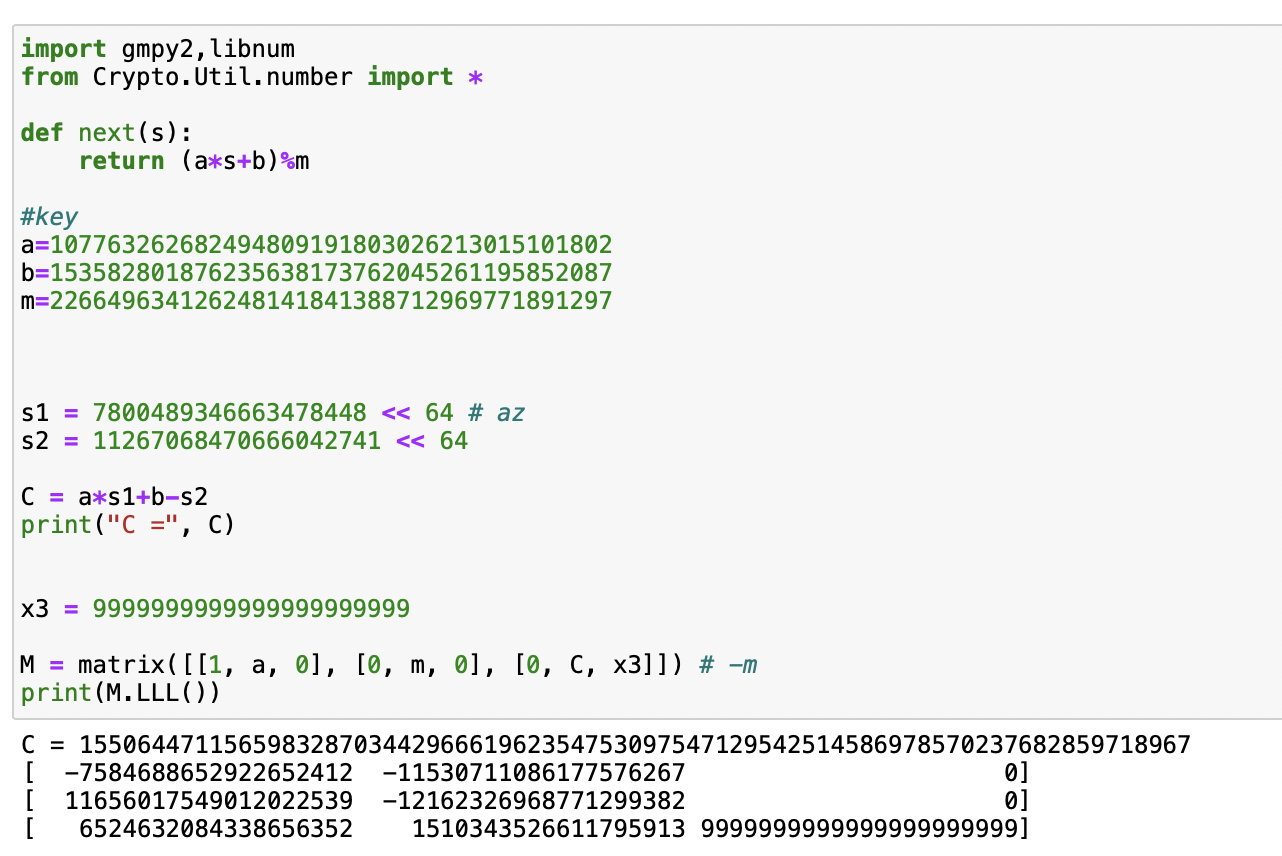
后经验证，$d_1、d_2$正确，可求解出flag，完整exp如下

from Crypto.Util.number import *
from Crypto.Cipher import AES

def next(s):
    return (a*s+b)%m

#key
a=107763262682494809191803026213015101802
b=153582801876235638173762045261195852087
m=226649634126248141841388712969771891297

# ct
ct = "e0e0702cb7d6fc19ace729befca40af50123f7a6ede1f3ae4b3a2acd7b1dd8371473105886afd15773441fa06c656ad6"
ct = b''.fromhex(ct)

s1 = 7800489346663478448 << 64 # az
s2 = 11267068470666042741 << 64

C = a*s1+b-s2
print("C =", C)


x3 = 9999999999999999999999

M = matrix([[1, a, 0], [0, m, 0], [0, C, x3]]) # -m
print(M.LLL())

d1, d2 = M.LLL()[-1][0], M.LLL()[-1][1]
s1 += d1
for i in range(19):
    s1 = next(s1)

key = next(s1) >> 64
key = (key << 64) + (next(next(s1)) >> 64)
key = long_to_bytes(key).ljust(16, b'\x00')
iv = long_to_bytes(next(next(next(s1)))).ljust(16, b'\x00')
cipher = AES.new(key, AES.MODE_CBC, iv)
flag = cipher.decrypt(ct)
print(flag.decode())
# npuctf{7ruc4t3d-L(G-4nd-LLL-4r3-1nt3r3st1ng}

正如huangx师傅所写道，这个格对数据大小要求严格，并不具备普适性.

笔者用题目代码生成另一组数据，却无法用此格正确规约出对应的$d_1、d_2$.

也确实，题目给了20组数据，仅用其中两组求解，注定了有其局限性.

通解

我们渴求通解，不避讳直觉，尽量严谨.

有：
$$
\begin{aligned} s_1+d_1 &= a•seed+b \mod m \\ s_2+d_2 &= a(s_1+d_1)+b \mod m \\s_3+d_3 &= a(s_2+d_2)+b \mod m \\s_4+d_4 &= a(s_3+d_3)+b \mod m \\ &\vdots \\ s_n+d_n&=a(s_{n-1}+d_{n-1})+b \mod m\end{aligned}
$$
于是:
$$
\begin{aligned} s_3+d_3 &= a(s_2+d_2)+b \\&= a(a(s_1+d_1)+b)+b \\ &= a^2d_1+a^2s_1+ab+b \mod m\\s_4+d_4 &= a(s_3+d_3)+b \\ &= a(a^2d_1+a^2s_1+ab+b )+b \\ &= a^3d_1+a^3s_1+a^2b+ab+b \mod m \end{aligned}
$$
我们试着归纳出$s_k+d_k$与$a_1、d_1$的关系，有:
$$
\begin{aligned} s_k+d_k &= a^{k-1}d_1+a^{k-1}s_1+b(a^{k-2}+a^{k-3}+···+1)\\ &= a^{k-1}d_1+a^{k-1}s_1+b•\frac{a^{k-1}-1}{a-1} \mod m\\
d_k&=a^{k-1}d_1+a^{k-1}s_1+b•\frac{a^{k-1}-1}{a-1}-s_k \\ &=A_kd_1+B_k \mod m \\ &=A_kd_1+B_k-K_im \end{aligned}
$$
把已知量总和一起记为$B_k$，方便后续构造.

值得注意的是，若已知量是在同余式中推出的，则应该对模取余.

这里为证实普适性，接下来笔者将用自己跑的数据来进行构造、求解.

题目数据

a=128545450633871437429437241254781148160
b=233389597015557833347401241174618011636
m=315065305238616866744968219610334118613
S = [7252977577629929975, 602943885393902321, 14518360259726210355, 6192947457464349552, 15019407963861094834, 14267673519450511986, 13311249722121495920, 4770531380593537313, 4016640960840138550, 7372256512820149548, 5309479576445491719, 8387322981994896008, 7719519419830748972, 14594645407993739304, 6422468239672604983, 16436109440098721169, 7623155229218776374, 5083416709024918086, 16792163486593697020, 14435467838685199929]
ct = "8946eaf25a529e48f3f561ff8cba7cf9"
ct = b''.fromhex(ct)

构造格

显然，这种思路下数据多，格的构造似乎变得复杂了起来.

但只要我们抓住准则$\vec v •M=\vec w$不松手，就能逐步构造出格.

由易到难，$\vec v •M=\vec w$中最好确定大部分元素的该是$\vec w$，往里面填充我们要求量即可， 如下：
$$
\vec w = \left(\begin {array}{c} d_1& d_2 & \cdots & d_n \end{array} \right)
$$
接下来，根据关系$d_k =A_kd_1+B_k-K_im$, 便可以逐步确定$\vec v 、 M$.

根据未知量放入$\vec v$, 已知量放入$M$， 再由构造的习惯，有如下:
$$
\vec v = \left(\begin {array}{c} d_1& 1 &-K_1 &-K_2& \cdots & -K_n \end{array} \right)
$$
那么$M$就很好确定了，如下：
$$
\left(\begin {array}{c} d_1& 1 &-K_1 &-K_2& \cdots & -K_n \end{array}\right)
\left(\begin {array}{c} A_1 & A_2 & \cdots & A_n\newline B_1 & B_2 & \cdots & B_n \newline m \newline &m \newline && \ddots \newline &&&m \end{array} \right)
=\left(\begin {array}{c} d_1& d_2 & \cdots & d_n \end{array} \right)
$$
其中M为n x (n+2)矩阵.

exp

import gmpy2

def A(k): # k从1开始
    return pow(a, k-1, m) # 需要%m

def B(k):
    return (a^(k-1)*S[1]+b*(a^(k-1)-1)*int(gmpy2.invert(a-1, m))-S[k])%m # 需要%m

def next(s):
    return (a*s+b)%m

a=128545450633871437429437241254781148160
b=233389597015557833347401241174618011636
m=315065305238616866744968219610334118613
S = [7252977577629929975, 602943885393902321, 14518360259726210355, 6192947457464349552, 15019407963861094834, 14267673519450511986, 13311249722121495920, 4770531380593537313, 4016640960840138550, 7372256512820149548, 5309479576445491719, 8387322981994896008, 7719519419830748972, 14594645407993739304, 6422468239672604983, 16436109440098721169, 7623155229218776374, 5083416709024918086, 16792163486593697020, 14435467838685199929]
ct = "8946eaf25a529e48f3f561ff8cba7cf9"
ct = b''.fromhex(ct)

S = [i<<64 for i in S]
S = ['占位']+S
M = matrix(len(S)+1,len(S)-1)
for i in range(1, len(S)):
    # 放A
    M[0,i-1]=A(i)
    
    # 放B
    M[1,i-1]=B(i)
    
    # 放m
    M[i+1,i-1]=m

for line in M.LLL():
    s = S[1]+abs(line[0])
    if (next(s)>>64)==(S[2]>>64):
        print(s)
        print("ok")
        break
        
for i in range(19):
    s = next(s)

key = next(s) >> 64
key = (key << 64) + (next(next(s)) >> 64)
key = long_to_bytes(key).ljust(16, b'\x00')
iv = long_to_bytes(next(next(next(s)))).ljust(16, b'\x00')
cipher = AES.new(key, AES.MODE_CBC, iv)
flag = cipher.decrypt(ct)
print(flag.decode())
# flag{123}

更多

当然，依据[2]、[3]， 我们还能构造满秩格子，便于验证与调整.

TL;DR

1. 为利用多组数据，我们需要找到各组之间的关系

2. 为寻得能用来构造格的关系式， 思路是要定住$\vec v$，也即固定未知量，便能指导构造关系式

   （本题中，表现为$d_i$都能用$d_1$表示，则固定未知量$d_1$，放入$\vec v$中，然后尝试把迭代式都用$d_1$，找规律以找到关系式来构造格）

3. 确定关系式后，利用准则$\vec v •M=\vec w$，初步确定格的构成

4. （可选）将格补充为方阵，根据Bounds灵活调参

5. LLL求出要求量

参考

[1] https://huangx607087.online/2021/02/06/LatticeNotes5/#toc-heading-11

[2] https://blog.csdn.net/figfig55/article/details/128069624

[3] https://www.anquanke.com/post/id/204846#h3-3

35c3CTF2019[unofficial]

题目

import os, math, sys, binascii
from secrets import key, flag
from hashlib import sha256
from Crypto.Cipher import AES

p = 21652247421304131782679331804390761485569
bits = 128
N = 40

if __name__ == '__main__':
    # key = keygen()   # generated once & stored in secrets.py
    challenge = keygen()
    print(' '.join(map(str, challenge)))
    response = int(input())
    if response != sum(x*y%p for x, y in zip(challenge, key)):
        print('ACCESS DENIED')
        exit(1)

    print('ACCESS GRANTED')
    cipher = AES.new(
            sha256(' '.join(map(str, key)).encode('utf-8')).digest(),
            AES.MODE_CFB,
            b'\0'*16)
    print(binascii.hexlify(cipher.encrypt(flag)).decode('utf-8'))

题解

就着上一题中更多里调整所指向的文章，按照跟着把题都走一遍的思路，笔者跟着参考[1]、[2]进行了复现

读题可知，题目分别生成了有N个数据的key、challenge，并给出了challenge.

然后计算
$$
response =\sum\limits^{n}_{i=1} (key_i•challenge_i\mod p)
$$
其后，要求输入response，如果满足如上关系，则输出ACCESS GRANTED,进行AES加密并给出密文；反之，输出ACCESS DENIED，程序终止.

事实上，原题中还有后缀为pcap的流量文件，经过一番操作，能在其中找到39组ACCESS GRANTED， 1组ACCESS DENIED的数据，而这些数据的key都是相同的，challenge不同.

但最初，笔者由于没看完整，以为题目只有一组数据，便进行了如下格相关的尝试，也一并记录.

格的尝试

对于题目关系式，有:
$$
\begin{aligned} response &= \sum\limits^{n}_{i=1} (key_i•challenge_i\mod p) \\&= (key_1•challenge_1\mod p)+\cdots+(key_n•challenge_n\mod p) \\&= (key_1•challenge_1-k_1p)+\cdots+(key_n•challenge_n-k_np)\\&=key_1•challenge_1+key_2•challenge_2+\cdots+key_n•challenge_n-Kp\end{aligned}
$$
于是，尝试构造出了如下$\vec v•M=\vec w$:
$$
\left(\begin {array}{c} key_1& key_2 & \cdots & key_n & -K &-1 \end{array}\right)
\left(\begin {array}{c} 1 &&&&challenge_1 \newline &1&&&challenge_2 \newline &&\ddots&&\vdots \newline &&&1&challenge_n \newline &&&&p \newline &&&&response \end{array} \right)
=\left(\begin {array}{c} key_1& key_2 & \cdots & key_n & 0 \end{array} \right)
$$
代码如下:

p = 21652247421304131782679331804390761485569
keys = [298539175337331255822704105154795432720, 87140312711560535519086100550511205417, 184565474844349422800783273599048425518, 322281095696764831303430402664544221782, 10400176126102731014865154526193609901, 311465050308096828975786552590023761047, 255543084918661041085926125287141045637, 79506218523423179907548173152929818342, 45127622693714341638449515791872751108, 189819995420542088052860112540829995739, 251374742294581828998093738126822163367, 203832280452324126328620582890495674996, 276981611438190156791305837293732442983, 288713927320477818592627903418003091123, 232311167516524001929598819486418980667, 157175040606779034199182197251072938366, 253212855985810816107007930574788462463, 335737146313567537712317087100578791078, 224883045916887966304785559524859262485, 297772449149619863804975952098453046285, 182833023906487083779397773842271383684, 86424278793790309842042746782700597387, 48331648015807044859719644455528004502, 84675795786570086326159698012985374357, 29110538972227458052024422940866622686, 253099757893796574225592257618792382437, 130537441163239093124605207456906834947, 322155896745895123492974744840882728867, 143101606987208560544898347284570832542, 80450319795726972707024923435125439685, 184065293786381762488571639852159810873, 205044465185924930804255180092585954074, 173665803192211371735475948882255227793, 123099426723362751771022368568165468623, 98466978851123638099977546944074974441, 31051100745015300309538145741109661945, 15910164152988070825459049904390353845, 252133565197849684576683589325162079216, 221213935179163593563144900557245217124, 91600573494280665083155798786110626030]
response = 447921450281780579254201675117968298414027

M = Matrix(len(keys)+2, len(keys)+1)

for i in range(len(keys)):
    M[i,i]=1
    M[i, -1]=keys[i]
M[-2, -1]=p
M[-1, -1]=response
    
for i in M.LLL():
    print(i)

肉眼可见，规约并不理想.

但也不是坏事，对格构造更熟练的同时，也知悉了些“常识”.

比如建立了直觉. 形如如下的格经过LLL后，会得到分量极小的结果（当然可以用Minkowski’s theorem证实）
$$
\left(\begin {array}{c} 1 &&&&challenge_1 \newline &1&&&challenge_2 \newline &&\ddots&&\vdots \newline &&&1&challenge_n \newline &&&&p \newline &&&&response \end{array} \right)
$$
又说回来，这些分量极小的结果基本都是0与$\pm1$，巧妙的契合了背包问题.

所以，我们得到结论：背包类格子并不能得到大数.

---

正途

仔细、完整读题后，为抓住重点、简化过程，对题目源码进行如下修改

import os, math, sys, binascii
flag = b'flag{2022-12-30-Harry0597}'
from hashlib import sha256
from Crypto.Cipher import AES

p = 21652247421304131782679331804390761485569
bits = 128
N = 40


def rand():
    return int.from_bytes(os.urandom(bits // 8), 'little')


def keygen():
    return [rand() for _ in range(N)]


if __name__ == '__main__':
    key = keygen()
    Cs = []
    Rs = []
    for i in range(N-1):
        challenge = keygen()
        Cs.append(challenge)

        response = sum(x * y % p for x, y in zip(challenge, key))
        Rs.append(response)
    cipher = AES.new(
        sha256(' '.join(map(str, key)).encode('utf-8')).digest(),
        AES.MODE_CFB,
        b'\0' * 16)
    print(key)
    print("Cs =", Cs)
    print("Rs =", Rs)
    print("ct =", "'"+binascii.hexlify(cipher.encrypt(flag)).decode('utf-8')+"'")

问题也就演变成了：对于40个未知数，我们只有39个方程，求解这40个未知数.

通过学习参考[2]，笔者了解到：

1. 非齐次线性方程组的解的情况和矩阵Challenge的秩有关
2. 欠定方程要么无解，要么便有无数个解
3. 可利用Sagemath对非齐次线性欠定方程组求特解

故此，有如下矩阵运算:
$$
challenge_{39\times 40} \times key_{40\times 1} = response_{39\times 1}
$$
而原题中，利用Sage求出的特解恰好就是key,可用来求解密文.

Sage求解代码如下

from Crypto.Cipher import AES
from hashlib import sha256

p = 21652247421304131782679331804390761485569
I = Integers(p)

Cs = []
Rs = []
ct = ''
ct=b''.fromhex(ct)

C = Matrix(I,Cs)
R = vector(I,Rs)
key = C.solve_right(R)  # 输出特解
key=list(key)
print(key)

cipher = AES.new(sha256(' '.join(map(str, key)).encode('utf-8')).digest(),AES.MODE_CFB,b'\0'*16)
flag = cipher.decrypt(ct)
print(flag)

更多

就出题而言，为了达到利用Sage求出的特解恰好就是key效果，出题人当是在利用sage等工具求得特解后，反代入题目源码中，生成密文.

TL;DR

• 建立用矩阵运算表达方程的思维
• 知悉Sage可以求解非齐次线性欠定方程组特解

参考

[1] https://holocircuit.github.io/2019/01/08/unofficial.html

[2] https://xz.aliyun.com/t/3776