Harry's Blog

温故知新

0%

格密码学习

发表于 更新于   阅读次数： Valine：
本文字数： 7.4k 阅读时长 ≈ 7 分钟
格｜Lattice 学习笔记.

格｜Lattice

定义

线性无关基向量$v_1, v_2, v_3, .. ., v_n$的所有整系数线性组合所形成的$n$维离散空间。

给定n维空间中一组线性无关向量，其整系数组合构成的集合称为格。

格上的点排布呈周期性规律。

2-dimension Lattice

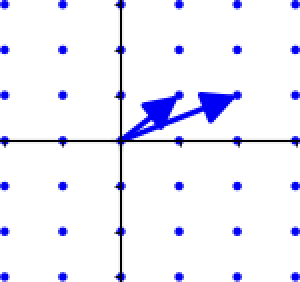
这里需要明确，不同的格基可能表示的是同一个格, 如下:

image-20221130231915760

为什么学格

为什么要学习，乃至于到致力于研究格的地步呢？

答案显而易见，因为格是困难的，好用的。

困难

先说困难性，准确说，应该是基于格基的数学问题是困难的，以至于可利用之构造抵抗量子计算机攻击的密码体系。

最直观的体会其困难性，有如下例子：

在二维格中找到格上一点，稍作移动使其离开格，给出这个不在格上的点，问原来的点位置几何？

这是好想象、也容易解决的问题，并不困难。

但实际上，当维度变到两三百的时候，就无法想象更难解决了。

好用

首先，得明确：在一定程度上，我们利用成熟的算法，能解决一些格难题。

那么，若我们能把其他难题规约到格难题上，再解决这个难题，就能破解原难题。

其次，还可以利用格来进行安全性证明。

格基等价变换

这里，若有线性代数的基础，想必是好理解的，若无则需来学学。

现，设我们有格基$v_1, v_2, v_3, .. ., v_n$，若进行如下初等变化(不改变行列式的值)，则新格基所生格与原来一样。

  1. 列向量交换：$v_i <——> v_j$

  2. 向量取反：$v_i <—— -v_i$

  3. 整系数线性组合：$v_i <—— v_i + k·v_j$

而以上操作，总能被简洁的总结为：格基矩阵右乘一个幺模矩阵（一种整数矩阵，其行列式的值为+1或-1，且幺模矩阵的逆还是幺模矩阵）

这有什么用呢？不妨考虑如下问题

任给两组格基，问它们所生成的格是否一致？

不难想到，有如下定理：

当且仅当两组格基满足$B_2=B_1U$（U为幺模矩阵）时，两组格基等价

于是，我们原问题等价于：$B_1^{-1}B_2$是否为幺模矩阵。得解。

格基本区域

格的基本区域可用基础平行多面体表示。

基础平行多面体 ｜ FUNDAMENTAL PARALLELEPIPED

给定格基，基础平行多面体$P(B) = \{a_1v_1,a_2v_2,\dots, a_nv_n | a_i\in[0,1) \}$ （注意：左闭右开）

可理解为格中最小重复单元。

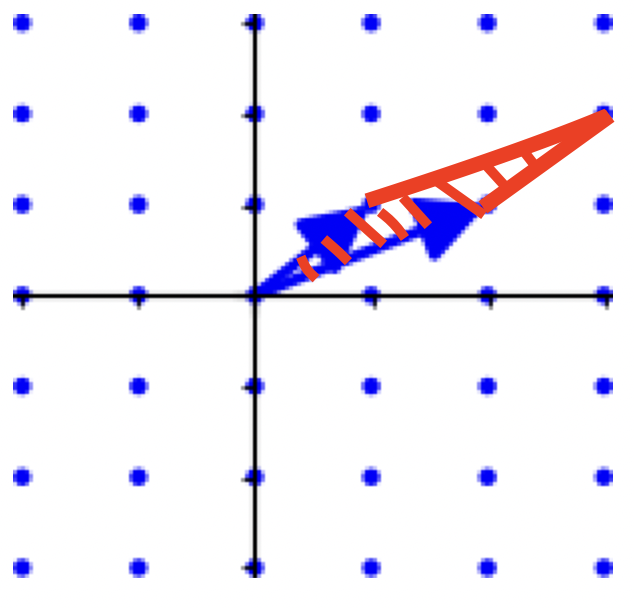
从二维格上理解，就是如下红色区域：

fundamental parallelepiped

显而易见，重复堆叠如上基础平行多面体，我们能找到所有的格点。

不仅如此，若我们在空间中任取一点k，我们都能将它映射到基础平行多面体中一个点上。

点k

映射

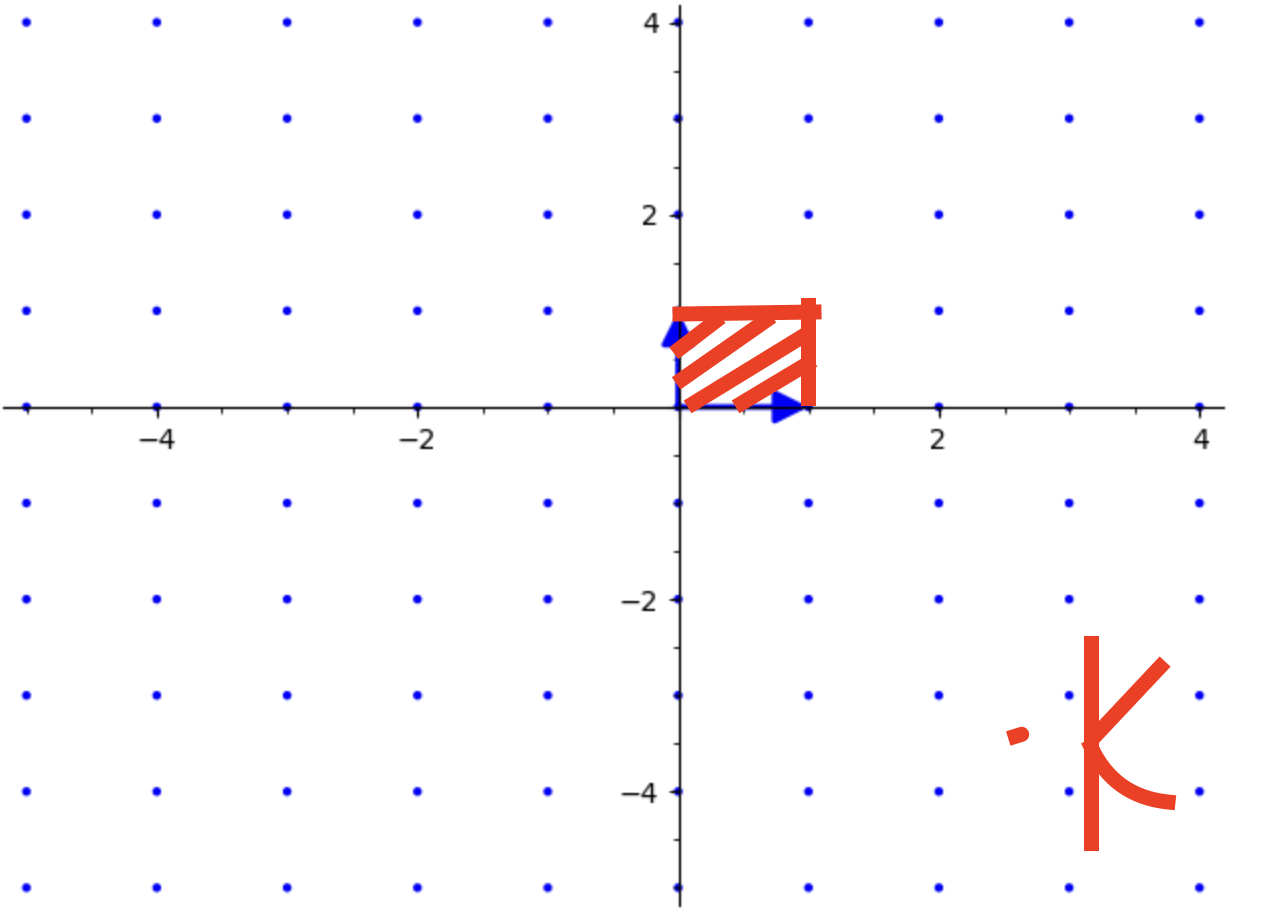
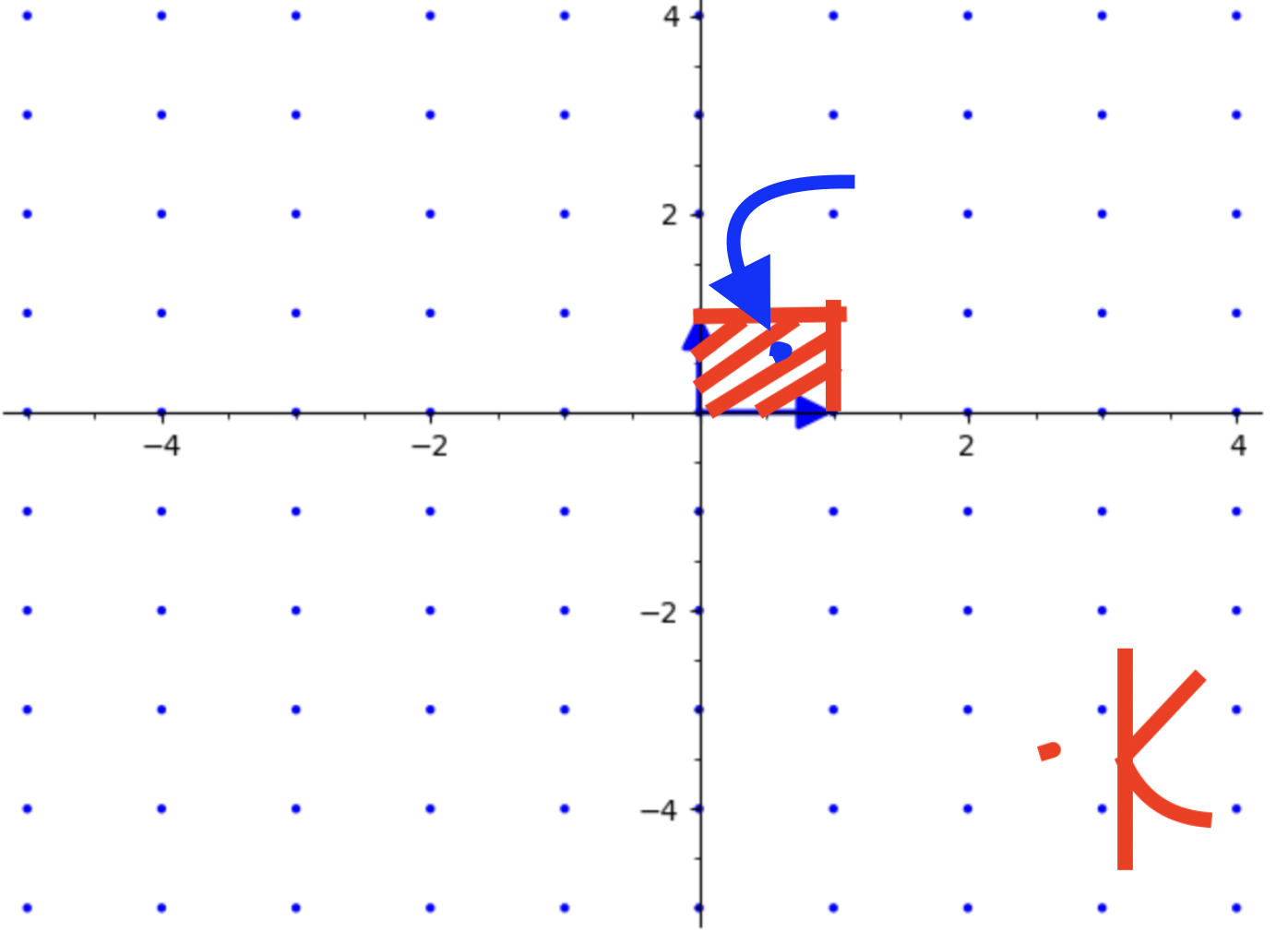
如上操作可归纳为：

$k=a_{1}v_{1}+…+a_{n}v_{n}$

映射：$k \mod P(B)=(a_1 \mod1)v_{1}+…+(a_{n} \mod 1)v_{n}$

那么，现在不妨考虑如下问题

任意给定 空间中一点k 与 格的基础平行多面体P(B)，问点k是否在格上？

有如上铺垫，不难想到，当$k \mod P(B)=(a_1 \mod1)v_{1}+…+(a_{n} \mod 1)v_{n}=0$，也即k映射到原点时，点k才在格上。

格的基本区域可用基础平行多面体表示。显然，格的基本区域并不唯一，以二维格为例，形状可以千奇百怪，但基础平行多面体的面积（更高维度则是体积）需一致。

基本区域不唯一

行列式

需要知道，行列式本质是数（标量），一种经过运算后所得到的数。

而这种运算的实际意义是：基向量构成的多面体的体积，也即基本区域的体积。

于是，便自然有了些推论：

  • 若多组格基生成的格都一致，那么这些格基所构成的行列式值都相等

    $$|det（BU)| = |det(B)det(U)|=|det(B)|$$

  • 考虑格的密度问题，当格基行列式值越小，则格点比较密集，密度较大

    也即：可用格基行列式值衡量格点密度（反相关）

延展空间｜span

我们称格 $L(B)$ 中基向量的所有线性组合所形成的集合为这组基向量所张成的延展空间(span)
$$
\mathop{span}(L(B)) = \mathop{span}(B)= \{a_1v_1,a_2v_2,\dots, a_nv_n | a_i\in R \}
$$
不妨思考如下问题

所有格的延展空间都是整个n维空间吗？

答案是显然的，不。

只有满秩格（秩的概念详见线性代数，这里满秩可简单理解为格基行列式的行数等于列数）的延展空间是整个n维空间。

此外，需注意辨析延展空间(SPAN)与基本区域(FUNDAMENTAL PARALLELEPIPED)的差异。

连续极小|successive minima

Successive minima，逐次最小长度，也可以叫为连续极小。

在学习这个概念之前，不妨先尝试回答如下问题

给定一个格，问其中最短向量的长度为？

或许一想到高维度的格，你就会觉得这个问题是难求解的。

但事实上，咬文嚼字后，其实你可以回答0，因为原点本身一定是格点，而最短向量长度则一定是0了。

但显然，这个命题除了提醒你该仔细起来外，没什么意义。

因此，在讨论最短向量时，我们一般找的是最短非零向量，而其长度一般用欧几里得范数表示。

定义

$\lambda_i(L)$

假设存在最小值$r$，使得能在半径为$r$的球内找到$i$个格点，且它们的延展空间为整个$i$维空间，则称这个$r$为$\lambda_i(L)$.

span

最重要的，得知道$\lambda_1(L)$指的是格L最短非零向量的长度。

施密特正交化｜Gram-Schmidt Orthogonalization

施密特正交化是线性代数中将一组基转化为正交基的运算过程.

GSO

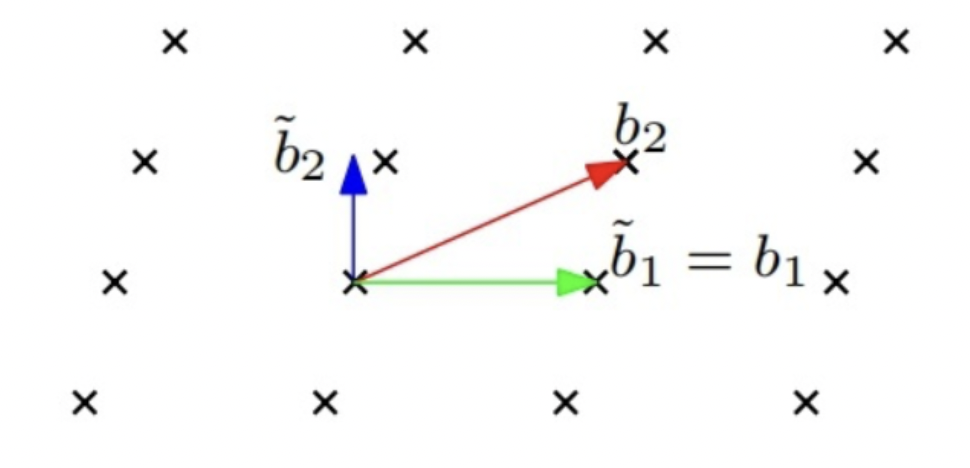
具体如下：

  1. 给定一组 n 个线性无关向量 $b_1,b_2,…,b_n$

  2. 计算，得到正交基$\widetilde{b_1},\widetilde{b_2},…,\widetilde{b_n}$

$$
\widetilde{b_1}=b_1\\ \widetilde{b_2}=b_2-\mu_{2,1}\widetilde{b_1},\mu_{2,1}={<b_2,\widetilde{b_1}>\over <\widetilde{b_1},\widetilde{b_1}>}\\ \vdots\\ \widetilde{b_i}=b_i-\sum^{i-1}\limits_{j=1}\mu_{i,j}\widetilde{b_j},\mu_{i,j}={<b_i,\widetilde{b_j}>\over <\widetilde{b_j},\widetilde{b_j}>}
$$

注：

  • $<b_i, \widetilde{b_j}>$表示$b_i$与$b_j$内积
  • $\mathop{pro}_{\widetilde{b_j}}{b_i}={<b_i,\widetilde{b_j}>\over <\widetilde{b_j},\widetilde{b_j}>}\widetilde{b_j}$, 表示$b_i$在$\widetilde{b_j}$上投影

此外，还可以进一步求出标准正交基：$\widetilde{b_1}/||\widetilde{b_1}||,\widetilde{b_2}/||\widetilde{b_2}||,…,\widetilde{b_n}/||\widetilde{b_n}||$

值得一提，施密特正交化能将基正交化，但并不能直接应用于格基，因为正交化过程中系数并没限制为整数，也就是 格基 施密特正交化后的结果很可能不在格上

QR分解｜QR decomposition

QR分解是施密特正交化的应用

对于格而言，先对格基间接施密特正交化（涉及系数四舍五入取整）后，得到近似正交基$\widetilde{b_1},\widetilde{b_2},…,\widetilde{b_n}$，然后构造如下矩阵

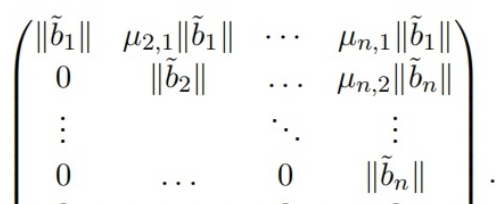
QR decomposition

本质上，QR分解形式的矩阵是格基的另一种矩阵表示法，上图中每个列向量都是格基

结论

  1. 因为QR分解矩阵是上三角，所以格基为$b_1,b_2,…,b_n$的格基本区域（行列式）就等于$||\widetilde{b_1}||,||\widetilde{b_2}||,…,||\widetilde{b_n}||$的乘积。

  2. $\lambda_1(L)>=\mathop{min}(||\widetilde{b_i}||)$

    $Proof：$

    最短非零向量能由这n组向量线性组合表示，而当最右下角的$||\widetilde{b_n}||$不为零（格的基本区域不为0，保证了这一点）时，纵使其上所有数都消为0，仍有$(0,0,…,\widetilde{b_n})$,也即：组出来的向量欧几里得长度一定大于等于$||\widetilde{b_n}||$

    所以最为理想的，当$||\widetilde{b_n}||=\mathop{min}(||\widetilde{b_i}||)$时，$\lambda_1(L)$最短可能是$\mathop{min}(||\widetilde{b_i})||$，其余情况一律大于之

    （更严谨的证明如下）

    image-20221203081933090

    总之，我们得到了$\lambda_1$下界。

闵可夫斯基定理｜Minkowski’s theorem

正如前文所述，通过QR分解，我们求得了$\lambda_1$下界(也即一个格中最短非零向量的长度下限).

而接下来所介绍的闵可夫斯基定理，将揭示出$\lambda_1$上界.

在学习闵可夫斯基定理之前，让我们先来了解Blichfeld定理.

Blichfeld定理 ｜ Blichfeld’s theorem

对于任意格$L$和一个大于格$L$基本区域体积的集合$S$，一定存在$z_1,z_2 \in S$, 满足$z_1-z_2 \in L$

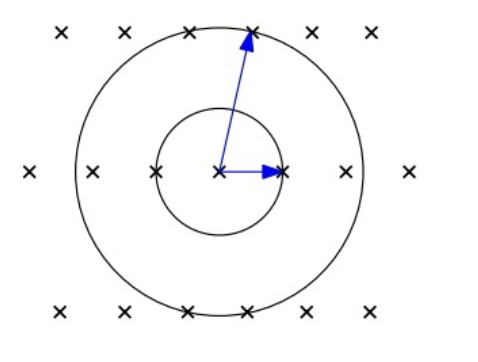
抽象的定理可以用直观图像来阐释，如下：

Blichfeld1

如上，讲座中选取了袋鼠🦘形状的集合S，因为单个S的面积大于基础区域，所以当S平铺在每个格点上时将会有重叠区域（袋鼠头尾相碰）.

显然，当两个格点相减所构成的向量（上图中红箭头）在格上。也易知，这个向量不会长于一个袋鼠最长的长度，也就是说：通过平移，我们总能在一个S的重叠区域中找到这个在格上的向量，如下图中蓝色箭头.

Blichfeld2

MINKOWSKI凸体定理｜MINKOWSKI’S CONVEX BODY THEOREM

设 Λ 为秩 n 的全秩格(满格)。对于任何中心对称凸集 S ，如果 $vol(S)>2^ndet(Λ)$ 则 S 包含一个非零格点。

直白说来，就是在格上任取一个集合满足如下条件的S，则S必然包含一个非零格点。

1.S是一个凸集合（否则总能巧妙的避开些点）

2.S的空间关于原点对称

3.如果S体积足够大，不仅要大于行列式，还要大于2^n乘行列式

Proof

​ 对于$\frac{S}{2}=\{x:2x\in S\}$，因为$vol(S)>2^ndet(Λ)$，所以$vol(\frac{S}{2})=2^{-n}vol(S)>det(Λ)$

​ 由Blichfeld定理，得：$\exists z_1、z_2 \in \frac{S}2{}$, 满足$z_1-z_2 \in Λ$.

​ 又因为$2z_1、2z_2、-2z_2(对称性) \in S$, 所以:$\frac{2z_1-2z_2}{2} = z_1-z_2 \in S$

​ 也即：S上存在一点（$2z_1、-2z_2$的中点）在Λ上

（证明思路可以多过几遍，注意体会Blichfeld定理中有向量在格上 和 MINKOWSKI凸体定理中有非零格点在格上差异）

MINKOWSKI第一定理｜MINKOWSKI’S FIRST THEOREM

$$
\lambda_1(Λ) \leq \sqrt{n} * \sqrt[n]{det(Λ)}
$$

挺重要的推论，这确定了格中最短非零向量的上界，这十分有助于我们寻找与验证最短非零向量。

MINKOWSKI第二定理｜MINKOWSKI’S SECOND THEOREM

$$
(\prod_{i=1}^{n} \lambda_i(Λ))^{\frac{1}{n}} \le \sqrt{n} * \sqrt[n]{det(Λ)}
$$

只做了解，不做介绍。

困难问题

区分、了解、学习格中困难问题很有必要。

首先，得会区分。

通过前文的讲述，我们能归纳出格中容易问题如下：

1.已知基和一个向量v，验证v是否在格L中

2.给定两组格基，判断两者生成的格是否等价

区分出容易问题后，我们接着来认识以下困难问题。

SVP｜shortest vector problem

最短向量问题：给定一个基为$B$的Lattice $L(B)$，找到一个这个基构成的格点，使得这个点距离0坐标点的距离最近.

SIVP（shortest independent vector problem）

最短独立向量问题：给定一个Lattice $L(B)$，找到n个线性独立的向量$x_1,…,x_n$并且这些向量的长度都要小于等于最长的最短向量$\lambda_n$.

CVP（closed vector problem）

最近向量问题：给定连续空间中任意的一个点$t$，找到距离点$t$最近的格点.

为了进一步体会、理解，这里介绍基于格的GGH加密体系

GGH

已死亡。

GGH的陷门在于求解CVP的困难性。

给定点$w$，若再给出正交性好的短基，能高效地用利用Babai’s Closest Vector algorithm求解CVP

Babai’s Closest Vector algorithm

大体思路

给定点w，基向量组为$[v_1, .., v_n]$, 算法的思路是在实数范围内找到$T$满足$w = t_1v_1+…+t_n*v_n$

然后对$T$中各元素四舍五入，来找到格上最靠近w点的向量$T’*basis$.

使用条件

要求给的格基短且正交性好（接近正交基），都满足的话能非常高效准确地求解.

而对于正交性差的格基，求解出来的结果基本是错误的.

代码实现

1
2
3
4
5
6
7
8
9
10
11
# https://gist.github.com/kelbyludwig/201d08e3e8e9a4f3764f366398f12a47
def babai(w, basis):
    """
    babai will approximate the closest lattice point formed by the supplied basis
    to the supplied vector w. babai only works well when given a "good" basis.
    """
    W = Matrix(RR, w)
    BR = basis.change_ring(RR) 
    T = BR.solve_left(W)
    C = vector(ZZ, [round(t) for t in T[0]])
    return C*basis

结合LLL后, Babai的最近平面算法

1
2
3
4
5
6
7
8
def babai(A, w):
    A = A.LLL()
    G = A.gram_schmidt()[0]
    t = w
    for i in reversed(range(A.nrows())):
        c = ((t * G[i]) / (G[i] * G[i])).round()
        t -= A[i] * c
    return w - t

正交性

我称格基接近最短正交基的程度为正交性，参考kelbyludwig的博客，可利用hadamard ratio来衡量正交性，详细如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def hadamard_ratio(basis):
    """
    hadamard_ratio returns the hadamard ratio of the supplied basis. the hadamard
    ratio is a number between 0 and 1 that quantifies the orthogonality of the
    baiss. The higher the hadamard ratio, the more orthogonal (read: better) the
    basis.
    """
    if len(basis.rows()) != len(basis.columns()):
        raise Exception("no non-square matrices allowed")
    BR = basis.change_ring(RR)
    d = BR.determinant()
    ls = [v.norm() for v in BR]
    l = reduce(lambda x,y: 1.0*x*y, ls)
    return (d/l)**(1.0/3.0)

GGH加解密

加密

具体的，GGH加密过程如下：

  1. 随机生成一个hadamard ratio高的格基s，作为私钥
  2. 将s乘随机生成的幺模矩阵，得到hadamard ratio低的格基B，作为公钥
  3. 将消息转换为向量$m$，再置入格中的点p($p=m*B$)
  4. 生成每个元素随机为±sigma（sigma默认为3，得较小）的扰动向量e
  5. 计算$c = p + e$，c作为密文

本质上，GGH加密就是把格中的信息向量给微移了，使得这个点不在格上了

解密

对应的，GGH解密过程如下：

  1. 有私钥s、密文c，利用Babai算法求出格上距离c最近的向量p
  2. $m = p/B$，解出明文m

精妙绝伦，因为无论格基B还是s，所对应的格都是相同的（所以对s的cvp结果等效于对B的cvp结果）

但利用s的正交性好可求解cvp的特点，把s做私钥，w做公钥实现陷门的构造。

Nyguen’s Attack

GGH公开没几年，发明者们为了证明其安全性在网上组织了挑战，并给了5组加密后的密文与公钥

Nyguen实现了攻击，把五组密文都给破解了，GGH发明者之一直呼：”今其亡矣！”

之前博客有说，LLL把背包打穿了个大口，而Nyguen’s Attack则直接杀死了GGH

参考

[1] https://space.bilibili.com/5277360/video

[2] http://www.zimablue.life/2022/05/04/Lattice-Lesson1/

[3] https://www.zhihu.com/column/c_1312093478458458112

[4] https://zhuanlan.zhihu.com/p/161622928

[5] https://kel.bz/post/lattices/