强网先锋

ASR

题目

from Crypto.Util.number import getPrime
# from secret import falg
"""
pad = lambda s:s + bytes([(len(s)-1)%16+1]*((len(s)-1)%16+1))

n = getPrime(128)**2 * getPrime(128)**2 * getPrime(128)**2 * getPrime(128)**2
e = 3

flag = pad(flag)
print(flag)
assert(len(flag) >= 48)
m = int.from_bytes(flag,'big')
c = pow(m,e,n)

print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
"""
import gmpy2
n = 8250871280281573979365095715711359115372504458973444367083195431861307534563246537364248104106494598081988216584432003199198805753721448450911308558041115465900179230798939615583517756265557814710419157462721793864532239042758808298575522666358352726060578194045804198551989679722201244547561044646931280001
p1 = 260594583349478633632570848336184053653
p2 = 223213222467584072959434495118689164399
p3 = 218566259296037866647273372633238739089
p4 = 225933944608558304529179430753170813347
phi = (p1**2 - p1)*(p2**2 - p2)*(p3**2 - p3)*(p4**2 - p4)
e = 3
c = 945272793717722090962030960824180726576357481511799904903841312265308706852971155205003971821843069272938250385935597609059700446530436381124650731751982419593070224310399320617914955227288662661442416421725698368791013785074809691867988444306279231013360024747585261790352627234450209996422862329513284149
print(e)
print(phi)

题解

yafu跑出各因子

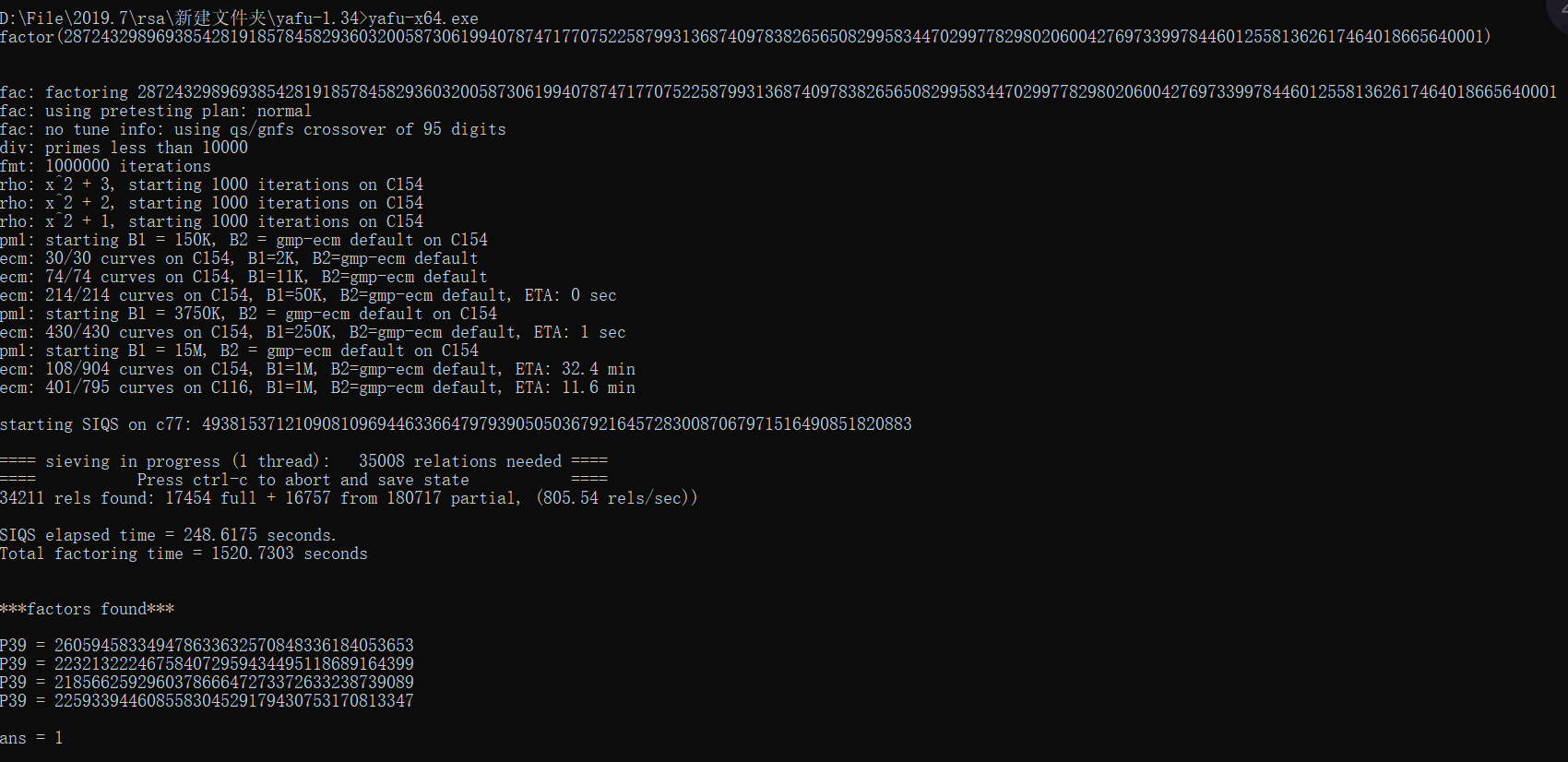
再有限域开三次方，即解。

#脚本2
#Sage
import libnum

n = 8250871280281573979365095715711359115372504458973444367083195431861307534563246537364248104106494598081988216584432003199198805753721448450911308558041115465900179230798939615583517756265557814710419157462721793864532239042758808298575522666358352726060578194045804198551989679722201244547561044646931280001
p1 = 260594583349478633632570848336184053653
p2 = 260594583349478633632570848336184053653
p3 = 223213222467584072959434495118689164399
p4 = 223213222467584072959434495118689164399
p5 = 218566259296037866647273372633238739089
p6 = 218566259296037866647273372633238739089
p7 = 225933944608558304529179430753170813347
p8 = 225933944608558304529179430753170813347

phi = (p1**2 - p1)*(p2**2 - p2)*(p3**2 - p3)*(p4**2 - p4)
e = 3
c = 945272793717722090962030960824180726576357481511799904903841312265308706852971155205003971821843069272938250385935597609059700446530436381124650731751982419593070224310399320617914955227288662661442416421725698368791013785074809691867988444306279231013360024747585261790352627234450209996422862329513284149

P.<a>=PolynomialRing(Zmod(p1),implementation='NTL')
A=a^e-c
mas=A.monic().roots()

P.<a>=PolynomialRing(Zmod(p2),implementation='NTL')
B=a^e-c
mbs=B.monic().roots()

P.<a>=PolynomialRing(Zmod(p3),implementation='NTL')
C=a^e-c
mcs=C.monic().roots()

P.<a>=PolynomialRing(Zmod(p4),implementation='NTL')
D=a^e-c
mds=D.monic().roots()

P.<a>=PolynomialRing(Zmod(p5),implementation='NTL')
E=a^e-c
mes=E.monic().roots()

P.<a>=PolynomialRing(Zmod(p6),implementation='NTL')
F=a^e-c
mfs=F.monic().roots()

P.<a>=PolynomialRing(Zmod(p7),implementation='NTL')
G=a^e-c
mgs=G.monic().roots()

P.<a>=PolynomialRing(Zmod(p8),implementation='NTL')
H=a^e-c
mhs=H.monic().roots()

for maa in mas:
    tmp1=maa[0]
    for mbb in mbs:
        tmp2=mbb[0]
        for mcc in mcs:
            tmp3=mcc[0]
            for mdd in mds:
                tmp4=mdd[0]
                for mee in mes:
                    tmp5=mee[0]
                    for mff in mfs:
                        tmp6=mff[0]
                        for mgg in mgs:
                            tmp7=mgg[0]
                            for mhh in mhs:
                                tmp8=mhh[0]
                                try:
                                    solution = CRT_list([int(tmp1), int(tmp2), int(tmp3), int(tmp4), int(tmp5), int(tmp6), int(tmp7), int(tmp8)], [p1,p2,p3,p4,p5,p6,p7,p8])
                                    flag = str(libnum.n2s(int(solution)))
                                    if 'flag' in flag:
                                        print(flag)
                                    if 'ctf' in flag:
                                        print(flag)
                                except:
                                    pass
# flag{Fear_can_hold_you_prisoner_Hope_can_set_you_free}\x06\x06\x06\x06\x06\x06'

flag{Fear_can_hold_you_prisoner_Hope_can_set_you_free}

polydiv

题目

poly2.py

class Polynomial2():
    '''
    模二多项式环，定义方式有三种
    一是从高到低给出每一项的系数
        >>> Polynomial2([1,1,0,1])
        x^3 + x^2 + 1

    二是写成01字符串形式
        >>> Polynomial2('1101')
        x^3 + x^2 + 1

    三是直接给出系数为1的项的阶
        >>> Poly([3,1,4])
        x^4 + x^3 + x
        >>> Poly([]) # 加法元
        0
        >>> Poly(0) # 乘法元
        1
        >>> Poly(1,2) * Poly(2,3)
        x^5 + x^3
    '''
    def __init__(self,ll):
        
        if type(ll) ==  str:
            ll = list(map(int,ll))

        self.param = ll[::-1]
        self.ones = [i for i in range(len(self.param)) if self.param[i] == 1] # 系数为1的项的阶数列表
        self.Latex = self.latex()
        self.b = ''.join([str(i) for i in ll]) # 01串形式打印系数
        
        self.order = 0 # 最高阶
        try:self.order = max(self.ones)
        except:pass
        
    def format(self,reverse = True):
        '''
            格式化打印字符串
            默认高位在左
            reverse = False时，低位在左
            但是注意定义多项式时只能高位在右
        '''
        r = ''
        if len(self.ones) == 0:
            return '0'
        if reverse:
            return ((' + '.join(f'x^{i}' for i in self.ones[::-1])+' ').replace('x^0','1').replace('x^1 ','x ')).strip()
        return ((' + '.join(f'x^{i}' for i in self.ones)+' ').replace('x^0','1').replace('x^1 ','x ')).strip()

    def __call__(self,x):
        '''
            懒得写了，用不到
        '''
        print(f'call({x})')

    def __add__(self,other):
        '''
            多项式加法
        '''
        a,b = self.param[::-1],other.param[::-1]
        if len(a) < len(b):a,b = b,a
        for i in range(len(a)):
            try:a[-1-i] = (b[-1-i] + a[-1-i]) % 2
            except:break
        return Polynomial2(a)

    def __mul__(self,other):
        '''
            多项式乘法
        '''

        a,b = self.param[::-1],other.param[::-1]
        r = [0 for i in range(len(a) + len(b) - 1)]
        for i in range(len(b)):
            if b[-i-1] == 1:
                if i != 0:sa = a+[0]*i
                else:sa = a
                sa = [0] * (len(r)-len(sa)) + sa
                #r += np.array(sa)
                #r %= 2
                r = [(r[t] + sa[t])%2 for t in range(len(r))]
        return Polynomial2(r)

    def __sub__(self,oo):
        # 模二多项式环，加减相同
        return self + oo


    def __repr__(self) -> str:
        return self.format()
    
    def __str__(self) -> str:
        return self.format()

    def __pow__(self,a):
        # 没有大数阶乘的需求，就没写快速幂
        t = Polynomial2([1])
        for i in range(a):
            t *= self
        return t
    
    def latex(self,reverse=True):
        '''
            Latex格式打印...其实就是给两位及以上的数字加个括号{}
        '''
        def latex_pow(x):
            if len(str(x)) <= 1:
                return str(x)
            return '{'+str(x)+'}'
        
        r = ''
        if len(self.ones) == 0:
            return '0'
        if reverse:
            return (' + '.join(f'x^{latex_pow(i)}' for i in self.ones[::-1])+' ').replace('x^0','1').replace(' x^1 ',' x ').strip()
        return (' + '.join(f'x^{latex_pow(i)}' for i in self.ones)+' ').replace('x^0','1').replace(' x^1 ',' x ').strip()

    def __eq__(self,other):
        return self.ones == other.ones

    def __lt__(self,other):
        return max(self.ones) < max(other.ones)

    def __le__(self,other):
        return max(self.ones) <= max(other.ones)

def Poly(*args):
    '''
        另一种定义方式
        Poly([3,1,4]) 或 Poly(3,1,4)
    '''
    if len(args) == 1 and type(args[0]) in [list,tuple]:
        args = args[0]
        
    if len(args) == 0:
        return Polynomial2('0')
    
    ll = [0 for i in range(max(args)+1)]
    for i in args:
        ll[i] = 1
    return Polynomial2(ll[::-1])

    
PP = Polynomial2
P = Poly
# 简化名称,按长度区分 P 和 PP
if __name__ == '__main__':
    p = Polynomial2('10011')
    print(p)
    p3 = Polynomial2('11111')
    print(p3)
    Q = p*p3
    print(Q)

task.py

import socketserver
import os, sys, signal
import string, random
from hashlib import sha256

from secret import flag
from poly2 import *

pad = lambda s:s + bytes([(len(s)-1)%16+1]*((len(s)-1)%16+1))
testCases = 40

class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self, prompt=b'> '):
        self.send(prompt, newline=False)
        return self._recvall()

    def close(self):
        self.send(b"Bye~")
        self.request.close()

    def proof_of_work(self):
        random.seed(os.urandom(8))
        proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
        _hexdigest = sha256(proof.encode()).hexdigest()
        self.send(f"sha256(XXXX+{proof[4:]}) == {_hexdigest}".encode())
        x = self.recv(prompt=b'Give me XXXX: ')
        if len(x) != 4 or sha256(x+proof[4:].encode()).hexdigest() != _hexdigest:
            return False
        return True

    def guess(self):
        from Crypto.Util.number import getPrime
        a,b,c = [getPrime(i) for i in [256,256,128]]
        pa,pb,pc = [PP(bin(i)[2:]) for i in [a,b,c]]
        r = pa*pb+pc
        self.send(b'r(x) = '+str(r).encode())
        self.send(b'a(x) = '+str(pa).encode())
        self.send(b'c(x) = '+str(pc).encode())
        self.send(b'Please give me the b(x) which satisfy a(x)*b(x)+c(x)=r(x)')
        #self.send(b'b(x) = '+str(pb).encode())
        
        return self.recv(prompt=b'> b(x) = ').decode() == str(pb)


    def handle(self):
        #signal.alarm(1200)

        if not self.proof_of_work():
            return

        for turn in range(testCases):
            if not self.guess():
                self.send(b"What a pity, work harder.")
                return
            self.send(b"Success!")
        else:
            self.send(b'Congratulations, this is you reward.')
            self.send(flag)
        
        

class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass

#class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
class ForkedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass

if __name__ == "__main__":
    
    HOST, PORT = '0.0.0.0', 10000
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

题解

工作量证明
模二多项式除法

代码实现了模二多项式乘法，且给出了$r = a*b+c$中的r、a、c，要求b

利用sage实现模二多项式除法，计算$b = (r-c)/a$，求解四十次，即解

import socket
import hashlib
# nc 182.92.223.176 42952
HOST = '182.92.223.176'
PORT = 42952

s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
s.connect((HOST, PORT))
data = ''.join(str(s.recv(1024)).strip("\n"))
sha_key = data[14:30]  # like: dygRhRVGRA146H43
sha_data = data[35:99]  # like: d06a5396ad875acdf0796cc5b0c083170e38728847085cfd99dadaeda71a3d17
print(data)
print(sha_key)
print(sha_data)
# 第一关 sha256
def decry(data):
    s = hashlib.sha256()  # Get the hash algorithm.
    s.update(data.encode())  # Hash the data.
    b = s.hexdigest()  # Get he hash value.
    return b
list1 = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J",
             "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U", "V", "W", "X", "Y", "Z", "a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o",
             "p", "q", "r", "s", "t", "u", "v", "w", "x", "y", "z", 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ]

def yi():
    for a in list1:
        for b in list1:
            for c in list1:
                for d in list1:
                    flag = "{0}{1}{2}{3}{4}".format(a, b, c, d, sha_key)
                    flag_sha = decry(flag)
                    flag1 = flag[0:4]
                    if str(flag_sha) == str(sha_data):
                        print(flag1)
                        print('恭喜！')
                        return str(flag1)

def set(r,a,c):
    ax = 0
    for i in a.split(' + '):
        if i == '1':
            ax += 1
        elif i == 'x':
            ax += x
        else:
            ax += x^int(i.replace('x^', ''))
    rx = 0
    for i in r.split(' + '):
        if i == '1':
            rx += 1
        elif i == 'x':
            rx += x
        else:
            rx += x^int(i.replace('x^', ''))
    cx = 0
    for i in c.split(' + '):
        if i == '1':
            cx += 1
        elif i == 'x':
            cx += x
        else:
            cx += x^int(i.replace('x^', ''))
    bx = (rx-cx)/ax
    return str(bx)

S.<x> = PolynomialRing(GF(2))
s_ = s.recv(1024)
s.send(yi().encode())
r = s.recv(1024)
ac = s.recv(1024)
r = str(r).split('= ')[-1].replace(r'\n', '')[:-1]
a = str(ac).split('= ')[1].split(r'\n')[0]
c = str(ac).split('= ')[2].split(r'\n')[0]
print(r)
print(a)
print(c)
ax = 0
for i in a.split(' + '):
    if i == '1':
        ax += 1
    elif i == 'x':
        ax += x
    else:
        ax += x^int(i.replace('x^', ''))
rx = 0
for i in r.split(' + '):
    if i == '1':
        rx += 1
    elif i == 'x':
        rx += x
    else:
        rx += x^int(i.replace('x^', ''))
cx = 0
for i in c.split(' + '):
    if i == '1':
        cx += 1
    elif i == 'x':
        cx += x
    else:
        cx += x^int(i.replace('x^', ''))
bx = (rx-cx)/ax
s.send(str(bx).encode())

print(s.recv(1024)) # succeess

tmp = s.recv(1024)
tmp = str(tmp)
tmp = tmp.split(r'= ')
r = tmp[1].replace(r'\na(x) ', '')
a = tmp[2].replace(r'\nc(x) ', '')
c = tmp[3].split(r'\n')[0]
ax = 0
for i in a.split(' + '):
    if i == '1':
        ax += 1
    elif i == 'x':
        ax += x
    else:
        ax += x^int(i.replace('x^', ''))
rx = 0
for i in r.split(' + '):
    if i == '1':
        rx += 1
    elif i == 'x':
        rx += x
    else:
        rx += x^int(i.replace('x^', ''))
cx = 0
for i in c.split(' + '):
    if i == '1':
        cx += 1
    elif i == 'x':
        cx += x
    else:
        cx += x^int(i.replace('x^', ''))
bx = (rx-cx)/ax
s.send(str(bx).encode())

print(s.recv(1024)) # succeess

for abcd in range(40):
    try:
        tmp = s.recv(1024)
        tmp = str(tmp)
        tmp = tmp.split(r'= ')
        print(tmp)
        r = tmp[1].replace(r'\na(x) ', '')
        a = tmp[2].replace(r'\nc(x) ', '')
        c = tmp[3].split(r'\n')[0]
        ax = 0
        for i in a.split(' + '):
            if i == '1':
                ax += 1
            elif i == 'x':
                ax += x
            else:
                ax += x^int(i.replace('x^', ''))
        rx = 0
        for i in r.split(' + '):
            if i == '1':
                rx += 1
            elif i == 'x':
                rx += x
            else:
                rx += x^int(i.replace('x^', ''))
        cx = 0
        for i in c.split(' + '):
            if i == '1':
                cx += 1
            elif i == 'x':
                cx += x
            else:
                cx += x^int(i.replace('x^', ''))
        bx = (rx-cx)/ax
        s.send(str(bx).encode())
        if i!=37:
            print(s.recv(1024)) # succeess
        else:
            print(s.recv(1024))
            print(s.recv(1024)) # flag
    except:
        pass
# b'Success!\nCongratulations, this is you reward.\nflag{08037511-8809-48ac-a54f-fca728f30089}\n'

flag{08037511-8809-48ac-a54f-fca728f30089}

Crypto

myJWT

题目

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.security.KeyPair;
import java.security.interfaces.ECPrivateKey;
import java.security.interfaces.ECPublicKey;
import java.security.*;
import java.util.Base64;
import java.util.Scanner;

import com.alibaba.fastjson.*;

class ECDSA{
	public KeyPair keyGen() throws Exception {
		KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("EC");
		keyPairGenerator.initialize(384);
		KeyPair keyPair = keyPairGenerator.genKeyPair();
		return keyPair;
	}
	
	public byte[] sign(byte[] str, ECPrivateKey privateKey) throws Exception {
		Signature signature = Signature.getInstance("SHA384withECDSAinP1363Format");
		signature.initSign(privateKey);
		signature.update(str);
		byte[] sig = signature.sign();
		return sig;
	}
	
	public boolean verify(byte[] sig, byte[] str ,ECPublicKey publicKey) throws Exception {
		Signature signature = Signature.getInstance("SHA384withECDSAinP1363Format");
		signature.initVerify(publicKey);
		signature.update(str);
		return signature.verify(sig);
	}
}

public class jwt{
	
	public static int EXPIRE = 60;
	public static ECDSA ecdsa = new ECDSA();
	public static String generateToken(String user, ECPrivateKey ecPrivateKey) throws Exception {
		JSONObject header = new JSONObject();
		JSONObject payload = new JSONObject();
		header.put("alg", "myES");
		header.put("typ", "JWT");
		String headerB64 = Base64.getUrlEncoder().encodeToString(header.toJSONString().getBytes());
		payload.put("iss", "qwb");
		payload.put("exp", System.currentTimeMillis() + EXPIRE * 1000);
		payload.put("name", user);
		payload.put("admin", false);
		String payloadB64 = Base64.getUrlEncoder().encodeToString(payload.toJSONString().getBytes());
		String content = String.format("%s.%s", headerB64, payloadB64);
		byte[] sig = ecdsa.sign(content.getBytes(), ecPrivateKey);
		String sigB64 = Base64.getUrlEncoder().encodeToString(sig);
		
		return String.format("%s.%s", content, sigB64);
	}
	
	public static boolean verify(String token, ECPublicKey ecPublicKey) throws Exception {
		String[] parts = token.split("\\.");
		if (parts.length != 3) {
			return false;
		}else {
			String headerB64 = parts[0];
			String payloadB64 = parts[1];
			String sigB64 = parts[2];
			String content = String.format("%s.%s", headerB64, payloadB64);
			byte[] sig = Base64.getUrlDecoder().decode(sigB64);
			return ecdsa.verify(sig, content.getBytes(), ecPublicKey);
		}
		
	}
	
	public static boolean checkAdmin(String token, ECPublicKey ecPublicKey, String user) throws Exception{
		if(verify(token, ecPublicKey)) {
			String payloadB64 = token.split("\\.")[1];
			String payloadDecodeString = new String(Base64.getUrlDecoder().decode(payloadB64));
			JSONObject payload = JSON.parseObject(payloadDecodeString);
			
			if(!payload.getString("name").equals(user)) {
				return false;
			}
			if (payload.getLong("exp") < System.currentTimeMillis()) {
				return false;
			}
			return payload.getBoolean("admin");
		} else {
			return false;
		}	
	}
	
	public static String getFlag(String token, ECPublicKey ecPublicKey, String user) throws Exception{
		String err = "You are not the administrator.";
		if(checkAdmin(token, ecPublicKey, user)) {
			File file = new File("/root/task/flag.txt");
			BufferedReader br = new BufferedReader(new FileReader(file));
			String flag = br.readLine();
			br.close();
			return flag;
		} else {
			return err;
		}
	}
	
	public static boolean task() throws Exception {
		Scanner input = new Scanner(System.in);
		System.out.print("your name:");
		String user = input.nextLine().strip();
		System.out.print(String.format("hello %s, let's start your challenge.\n", user));
		KeyPair keyPair = ecdsa.keyGen();
		ECPrivateKey ecPrivateKey = (ECPrivateKey) keyPair.getPrivate();
		ECPublicKey ecPublicKey = (ECPublicKey) keyPair.getPublic();
		String menu = "1.generate token\n2.getflag\n>";
		Integer choice = 0;
		Integer count = 0;
		while (count <= 10) {
			count++;
			System.out.print(menu);
			choice = Integer.parseInt(input.nextLine().strip());
			if(choice == 1) {
				String token = generateToken(user, ecPrivateKey);
				System.out.println(token);
			} else if (choice == 2) {
				System.out.print("your token:");
				String token = input.nextLine().strip();
				String flag = getFlag(token, ecPublicKey, user);
				System.out.println(flag);
				input.close();
				break;
			} else {
				input.close();
				break;
			}
		}
		return true;
	}
	
	public static void main(String[] args) throws Exception {
		task();
	}
	
}

题解

考点在于cve-2022-21449中ECDSA签名校验不对r,s是否为0零判断

那么，只需要

改admin为true
将exp时间改大
第三部分，签名部分构造并发送（0,0），即十六进制下0000
按题目要求对各部分内容编码

如上构造好token，交互时对应输入好name，即解

import base64
import time
# pt1 = b'eyJ0eXAiOiJKV1QiLCJhbGciOiJteUVTIn0='
# pt2 = b'eyJpc3MiOiJxd2IiLCJuYW1lIjoiYWRtaW4iLCJhZG1pbiI6ZmFsc2UsImV4cCI6MTY1OTE4MzQyMDY0Mn0='
# sig = b'UP7MD8__8dXBlkiO_UlSlamsS9obariYmRaB28zQimgKcJLc7XNNzVjhptkqG9BANFacQrxSVWU2cdL1lrYxvm1rZEtN4zHc79x3vsBX0zi5ohTAm3CWZgzT5bgzj52y'
pt1= b'{"typ":"JWT","alg":"myES"}'
pt2 = b'{"iss":"qwb","name":"admin","admin":true,"exp":99999999999999}'
pt3 = base64.b64encode(bytes.fromhex(r'0000'))
print(base64.b64encode(pt1).decode(), end='.')
print(base64.b64encode(pt2).decode(), end='.')
print(pt3.decode())

output

(base) wenhui@Caliburn ~ % nc 47.104.76.78 23334
your name:admin
hello admin, let's start your challenge.
1.generate token
2.getflag
>2
your token:eyJ0eXAiOiJKV1QiLCJhbGciOiJteUVTIn0=.eyJpc3MiOiJxd2IiLCJuYW1lIjoiYWRtaW4iLCJhZG1pbiI6dHJ1ZSwiZXhwIjo5OTk5OTk5OTk5OTk5OX0=.AAA=
flag{cve-2022-21449_Secur1ty_0f_c0de_1mplementation}

flag{cve-2022-21449_Secur1ty_0f_c0de_1mplementation}

Factor

题目

#encoding:utf-8
from Crypto.Util.number import *
from gmpy2 import *
from random import randint
from flag import flag

def gen1():
	r = 2
	while True:
		p2 = getPrime(1792)
		p1 = getPrime(1792)

		q1 = getPrime(512)
		q2 = getPrime(512)

		if (abs(p1-p2) < (p1//(2*r*q1*q2))):
			n1, n2 = (p1**r)*q1, (p2**r)*q2
			break

	phi1 = (p1**(r-1))*(p1-1)*(q1-1)
	phi2 = (p2**(r-1))*(p2-1)*(q2-1)
	while True:
		e1 = randint(5, (p1-1)*(q1-1))
		e2 = randint(5, (p2-1)*(q2-1))
		if gcd(e1, e2) == 1 and gcd(phi1, e1) == 1 and gcd(phi2, e2) == 1:
			break
	return n11, n12, e11, e12


def gen2():
	r = 7
	while True:
		p = getPrime(512)
		q =getPrime(512)
		N = (p**r)*q
		if len(bin(N)) == 4096:
			break

	idx = (r*(r-1)) / ((r+1)*(r+1))
	delta = int(pow(mpz(N), idx))
	phi = (p**(r-1))*(p-1)*(q-1)

	while True:
		d1 = getPrime(int(2048*idx)//2)
		d2 = getPrime(int(2048*idx)//2)
		if abs(d1-d2) < delta:
			m1 = invert(d1, phi)
			m2 = invert(d2, phi)
			break

	e2 = 0x10001
	return n2, e2, m1, m2

def gen3():
	r = 7
	while True:
		p = getPrime(512)
		q = getPrime(512)
		N = (p**r)*q
		phi = (p**(r-1))*(p-1)*(q-1)

		if len(bin(N))-2 == 4096:
			break

	r = 7
	idx = (r*(r-1)) / ((r+1)*(r+1))
	delta = int(pow(mpz(N), idx))

	while True:
		b = getRandomNBitInteger(int(2048*idx)//2)
		a = getRandomNBitInteger(int(2048*idx)//2)
		if a*b < delta:
			e3 = invert(a, phi)*b
			return n3, e3, b


n11, n12, e11, e12 = gen1()
print(f"n11={n11}\nn12={n12}\ne11={e11}\ne12={e12}\n")
n2, e2, m1, m2 = gen2()
print(f"n2={n2}\ne2={e2}\n")
n3, e3, b = gen3()
print(f"n3={n3}\ne3={e3}\n")

m3 = bytes_to_long(flag)
c11 = powmod(m1, e11, n11)
c12 = powmod(m2, e12, n12)
c2 = powmod(b, e2, n2)
c3 = powmod(m3, e3, n3)
print(f"c11={c11}\nc12={c12}\nc2={c2}\nc3={c3}\n")
'''
n11=801049932940568005269978912396585741498810389425615966036828877784238116634177290247194019425111606811005728521368879065336038221361037062407029836155148874719789714345603547779284558101833801155509762818376470874215789574939002212274399950433269775325144015468620263028557804618774240232988157961712628677901130814703917513004114547234375629747176834581166306552311075522669403347828095831520693563291249869832390698646691647204371133362254846234990175138047928703289833460734235302093916147489509206061923877623300596194317059884824322527532662470348274079800781120104946546063500763852622187404608639542858285661288293918912184354236687975919510300221932074135531028314170475917110204254042336116619335841213418990605590620842511615815443114612333881430920769002933370887494558640833005339906706603497809846863863967391543647049224309556936909768179259581851520214669904560467640473144481633920438487615788689262961741053146610554997224861331949716721056553499531186695425439163222802917813140266513735841447717418846360096652592844940362932171019143434080184728093326143821165097895058935372215708948088248596585127475770021962501262915274497478428868130455122612016408381607561200802267038869516896665387576895570245272035575637
e11=1898839980562048754607069073527844852132536432440793106124181406514770178066775988232362054809850074774981836898118651469424148725970708199461113088705044905633592578936333918328544505910996746428679299419879472444790941363558025887620570856598548320246426354974395765243741646121743413447132297230365355148066914830856904433750379114692122900723772114991199979638987571559860550883470977246459523068862898859694461427148626628283198896659337135438506574799585378178678790308410266713256003479022699264568844505977513537013529212961573269494683740987283682608189406719573301573662696753903050991812884192192569737274321828986847640839813424701894578472933385727757445011291134961124822612239865
n12=635401970340205725139325006504978344512744926958688031423448003992072769931808217486709574151492230879374574313457662436423263437792389711379687512056391117410807565492548718691166183372633151644917135272259770997096195518489056319350258673723095417922153182423913759272893696867426193704479752772511081457729513843682588951499551132432923147997238597538055902932123792252593514225328196541483451747314048080824405530742533473914329294346486691684904100406972073037050089861816604505650042953778360621934380815999541183067585498606053857125775979915077329566722531830089714823979965934190338538564188253271016367299890015449611141166780048763403252309160517164569110740561584100839212138661881615351382946813818078899882595313362934594951895560189003438775450675343590147821186953526262224973333962454561275321925151619178204499342339749637758100126893330994252902926509705617882239610380420830791088907378397226817514095468815228186716220057075095711894070032344613244803934541318573847029365563159918970404057137270884587905766828750387753130065274147902379993224780149663600462492281891320702134153853359393588902750423972068679293373333869389393970353760507436913233657422185531482023237384247535554666481760197851108297145147371
e12=1262647419018930022617189608995712260095623047273893811529510754596636390255564988827821761126917976430978175522450277907063247981106405519094560616378241247111698915199999363948015703788616554657275147338766805289909261129165025156078136718573006479030827585347458143645738353716189131209398056741864848486818076440355778886993462012533397208330925057305502653219173629466948635110352752162442552541812665607516753186595817376029707777599029040724727499952161261179707271814405907165207904499722122779096230563548011491932378429654764486855147873135769116637484240454596231092684424572258119768093562747249251518965380465994055049411715353547147466711949391814550591591830515262296556050946881

n2=209798341155088334158217087474227805455138848036904381404809759100627849272231840321985747935471287990313456209656625928356468120896887536235496490078123448217785939608443507649096688546074968476040552137270080120417769906047001451239544719039212180059396791491281787790213953488743488306241516010351179070869410418232801398578982244984544906579574766534671056023774009163991804748763929626213884208260660722705479782932001102089367261720194650874553305179520889083170973755913964440175393646890791491057655226024046525748177999422035469428780228224800114202385209306803288475439775037067014297973202621118959024226798935588827359265962780792266516120013602384766460619793738405476219362508944225007365127768741191310079985425349292613888185378948854602285379329682053663283534930182589905986063348509703027498270111412063194971956202729807710253369312175636837558252924035002153389909587349043986253518050303628071319876207392440085675892353421232158925122721273720564784886530611286461575045181073744696415657043278123662980166364494583141297996445429477446442693717498789391918530672770193730629928408766563592081857706608049076318165712479742423149330311238462044666384622153280310696667586565906758451118241914402257039981388209
e2=65537

n3=539779851369541956878655738599584730199799866957191805784596190682932284216781781433367450841202917758999300635019369629627621029957135109806205877317954671312041249493462048283611940752235036153024920172209763260723728345918562258401803973624430150143563078517485996070862532682695228590709019451174548520135142052216785774589096706631010293690859363524584240662502290912412366366114571976050857239915691266377257797199583543940504695517331512813468837128344612227973709974625418257243011036826241599265375741977853552204640800449679679351666009764297016524814036295707311913711955324055690490892097177271718850857268982130811714517356073266905474635370690445031512184247179039751734276906533177939993769044135143389748416635981226449566039039202521305851567296884751935162651063209779647359922622084851547605090230221057349511482738300221222563908357379545905837110168948295030747460300104202323692732549831403834387939156877086852393515817984772384147449841124275061609701453997579569931391166586163299940486204581696722731952467570857217406030804590055255431828403195798003509083922294733709507134156466158642941338493323430671502043066148246348074878064089651235355282144209668143249348243220714471988019011613749340243917652821
e3=8179300978753084587812861894047395225516049110376948812109811319430275614612773726672345893359691900281432484382670047044697374818043512731533402576374645405477207239801498428774783768163880078495448747421425078521981578408638790336528372019271073712013371141939808017049399434858687299480461753638164719404612128939787055797762174745092074547412183349192156638711750872083313795551439465507724807626674514935170104573715458782366469587138508845980490673890245713729782917089910271980557159592807350504157192913530007199510144004848020221181558472160543018733124225266127379373751910439604459368078652499029070936707349862139053913745186413782066470461478961703013591655136140060879250067379283913798867648758171004535775565306842444545755351202796833177560656564652632975685912935281581268141803696686952259539945588609591385807620108279333498170028167338690235117003515264281843953984997958878272347778561933726792473981855755454522886321669676790813189668084373153897754540290867346751033567500922477317530445967753955221454744946208555394588111484610700789566547507402309549957740815535069057837915204852490930168843605732632328017129154852857227895362549146737618906180651623216848500491438142456250653458053922622240299736136335179639180898730269690699965799644757774472147210271111150769048976871249731156387939260749192370361488285775377622944817570292095201906142567403539151179209316853493906909989301225903409448461436855145

c11=18979511327426975645936984732782737165217332092805655747550406443960209507493506811471688957217003792679188427155591583024966608843371190136274378868083075515877811693937328204553788450031542610082653080302874606750443090466407543829279067099563572849101374714795279414177737277837595409805721290786607138569322435729584574023597293220443351227559400618351504654781318871214405850541820427562291662456382362148698864044961814456827646881685994720468255382299912036854657082505810206237294593538092338544641919051145900715456411365065867357857347860000894624247098719102875782712030938806816332901861114078070638796157513248160442185781635520426230183818695937457557248160135402734489627723104008584934936245208116232179751448263136309595931691285743580695792601141363221346329077184688857290503770641398917586422369221744736905117499140140651493031622040723274355292502182795605723573863581253354922291984335841915632076694172921289489383700174864888664946302588049384130628381766560976143458735712162489811693014419190718601945154153130272620025118408017441490090252674737105557818759190934585829634273698371996797545908125156282869589331913665938038870431655063063535672001112420959158339261862052308986374193671007982914711432579
c12=336587005671304527566745948355290412636261748969581976214239578621816863343117433524033533838636941679300497270909696775021031004312477997130741361709262822736904340641138652359632950455651920464042448022467664596484055174270895170499076347333381222768518599018520948098943626229061996126260154604038101543546588917619576702866444998578555907070990331574722135141778182631559802154493815687284077524469331290249057291163803290619701104007028836609832847351748020354798788508790258935718399783002069490123663345156902440501507117289747695510266461539019431610123351176227443612317037899257774045751487135646052309277098939919088029284437221840182769808850184827681307611389353392683707516141736067793897378911235819049432542758429901945202632117089595899280390575706266239252841152490534353760118231918190110043319877744119083811214707593122757409240645257409097436061825613686773916466122693168971062418046703969144004779270391320645495586024342668002497155358623795942692477164489475917351003149045087283510728981096449890130735055015075557614253867698702479920619299919816768972581273507837309179450374634916567083251630203067065663910073926990517108921490442919372774170201239734064819301693527366233007925670043499415100789027665
c2=18352572608055902550350386950073774530453857897248738030380007830701135570310622004368605208336922266513238134127496822199799761713782366178177809597137102612444147565578155260524747439899150012223027218489946124086276814899675563837669559795153349686434242738207425653079514376089070980797596457151965772460109519623572502109592612394316680202287712465721767341302234806130244551387296133051760893033194962691942040228545508895009195291106297581470066545991352668826197346830561010198417527057944507902143965634058848276017283478933675052993657822322866778994956205033704582047618324071045349072526540250707463112668579342537349567247810715604220690215313641329522674080146047291570752430231923566302463491877377617044768978997438596643458475128936850994934029476030136643053997549253792076260765459166618369864942681056864815996253315631930002738854235841120321870075261782250357506436825550088826469396508045912258303652912217151127280959435741419961721418428605515096160344688795655562889755165362006775317188009008288782691705879510655892181975003485714604340542378477388225736316682379616676770234557939471098919647053799313777248678455620231721202780830980063824003076308811540534492317719811588898727134190545533822501681653
c3=113097822337683973761068913398570777162211043704088253732500045618770280334319497174908657828372816818344430304314992760410247741225285170975119344962728883084314382093407445567724674775086423808679124143380073906159023182353116556175251427048715466914368972746661938211846262612414049036821553068430149530397389927209475908905748728402722287875974303298260579839357610962198145974153609818939841880084892796820949226354126424023144300953584658958900737493704530725894948802258740332090822797815745616247879170037794873059391625680745994045522420168248552864215035136318711240256011217929372430302003068882829637056296413462078222453765071094277727760527662423010417144554652783429899139309180017349156600053882338180319473460877576898373222480215735280046214925463242092830060830764299787309912687294672319845054775281463150375545716818434962456139485501224661520991156961587158843064393883274763714930309353593180897123378717852182761518709151878662808890356934477932099818218743384674756674800089177733447066489275506387382342429495897972218764782517198727316942685748481956118012927027254979181519862451112593068440686462293151078537886822555211870303467014484443432209106264020502334805536091587252238173816637270028678636848763

'''

题解

共有三关

连分数分解n11、n12，解出m1、m2

import gmpy2
import libnum
from tqdm import tqdm
n11=801049932940568005269978912396585741498810389425615966036828877784238116634177290247194019425111606811005728521368879065336038221361037062407029836155148874719789714345603547779284558101833801155509762818376470874215789574939002212274399950433269775325144015468620263028557804618774240232988157961712628677901130814703917513004114547234375629747176834581166306552311075522669403347828095831520693563291249869832390698646691647204371133362254846234990175138047928703289833460734235302093916147489509206061923877623300596194317059884824322527532662470348274079800781120104946546063500763852622187404608639542858285661288293918912184354236687975919510300221932074135531028314170475917110204254042336116619335841213418990605590620842511615815443114612333881430920769002933370887494558640833005339906706603497809846863863967391543647049224309556936909768179259581851520214669904560467640473144481633920438487615788689262961741053146610554997224861331949716721056553499531186695425439163222802917813140266513735841447717418846360096652592844940362932171019143434080184728093326143821165097895058935372215708948088248596585127475770021962501262915274497478428868130455122612016408381607561200802267038869516896665387576895570245272035575637
e11=1898839980562048754607069073527844852132536432440793106124181406514770178066775988232362054809850074774981836898118651469424148725970708199461113088705044905633592578936333918328544505910996746428679299419879472444790941363558025887620570856598548320246426354974395765243741646121743413447132297230365355148066914830856904433750379114692122900723772114991199979638987571559860550883470977246459523068862898859694461427148626628283198896659337135438506574799585378178678790308410266713256003479022699264568844505977513537013529212961573269494683740987283682608189406719573301573662696753903050991812884192192569737274321828986847640839813424701894578472933385727757445011291134961124822612239865
n12=635401970340205725139325006504978344512744926958688031423448003992072769931808217486709574151492230879374574313457662436423263437792389711379687512056391117410807565492548718691166183372633151644917135272259770997096195518489056319350258673723095417922153182423913759272893696867426193704479752772511081457729513843682588951499551132432923147997238597538055902932123792252593514225328196541483451747314048080824405530742533473914329294346486691684904100406972073037050089861816604505650042953778360621934380815999541183067585498606053857125775979915077329566722531830089714823979965934190338538564188253271016367299890015449611141166780048763403252309160517164569110740561584100839212138661881615351382946813818078899882595313362934594951895560189003438775450675343590147821186953526262224973333962454561275321925151619178204499342339749637758100126893330994252902926509705617882239610380420830791088907378397226817514095468815228186716220057075095711894070032344613244803934541318573847029365563159918970404057137270884587905766828750387753130065274147902379993224780149663600462492281891320702134153853359393588902750423972068679293373333869389393970353760507436913233657422185531482023237384247535554666481760197851108297145147371
e12=1262647419018930022617189608995712260095623047273893811529510754596636390255564988827821761126917976430978175522450277907063247981106405519094560616378241247111698915199999363948015703788616554657275147338766805289909261129165025156078136718573006479030827585347458143645738353716189131209398056741864848486818076440355778886993462012533397208330925057305502653219173629466948635110352752162442552541812665607516753186595817376029707777599029040724727499952161261179707271814405907165207904499722122779096230563548011491932378429654764486855147873135769116637484240454596231092684424572258119768093562747249251518965380465994055049411715353547147466711949391814550591591830515262296556050946881
c11=18979511327426975645936984732782737165217332092805655747550406443960209507493506811471688957217003792679188427155591583024966608843371190136274378868083075515877811693937328204553788450031542610082653080302874606750443090466407543829279067099563572849101374714795279414177737277837595409805721290786607138569322435729584574023597293220443351227559400618351504654781318871214405850541820427562291662456382362148698864044961814456827646881685994720468255382299912036854657082505810206237294593538092338544641919051145900715456411365065867357857347860000894624247098719102875782712030938806816332901861114078070638796157513248160442185781635520426230183818695937457557248160135402734489627723104008584934936245208116232179751448263136309595931691285743580695792601141363221346329077184688857290503770641398917586422369221744736905117499140140651493031622040723274355292502182795605723573863581253354922291984335841915632076694172921289489383700174864888664946302588049384130628381766560976143458735712162489811693014419190718601945154153130272620025118408017441490090252674737105557818759190934585829634273698371996797545908125156282869589331913665938038870431655063063535672001112420959158339261862052308986374193671007982914711432579
c12=336587005671304527566745948355290412636261748969581976214239578621816863343117433524033533838636941679300497270909696775021031004312477997130741361709262822736904340641138652359632950455651920464042448022467664596484055174270895170499076347333381222768518599018520948098943626229061996126260154604038101543546588917619576702866444998578555907070990331574722135141778182631559802154493815687284077524469331290249057291163803290619701104007028836609832847351748020354798788508790258935718399783002069490123663345156902440501507117289747695510266461539019431610123351176227443612317037899257774045751487135646052309277098939919088029284437221840182769808850184827681307611389353392683707516141736067793897378911235819049432542758429901945202632117089595899280390575706266239252841152490534353760118231918190110043319877744119083811214707593122757409240645257409097436061825613686773916466122693168971062418046703969144004779270391320645495586024342668002497155358623795942692477164489475917351003149045087283510728981096449890130735055015075557614253867698702479920619299919816768972581273507837309179450374634916567083251630203067065663910073926990517108921490442919372774170201239734064819301693527366233007925670043499415100789027665

c = continued_fraction(Integer(n11) / Integer(n12))
for i in tqdm(range(1, 9999)):
    q12 = c.denominator(i)
    q11 = c.numerator(i)
    if gmpy2.gcd(n11, q11) != 1:
        print('q11 =', q11)
    if gmpy2.gcd(n12, q12) != 1:
        print('q12 =', q12)
        break
p11 = gmpy2.iroot(n11//q11,2)[0]
p12 = gmpy2.iroot(n12//q12,2)[0]
r = 2
phi11 = (p11**(r-1))*(p11-1)*(q11-1)
phi12 = (p12**(r-1))*(p12-1)*(q12-1)
d11 = int(gmpy2.invert(e11, phi11))
d12 = int(gmpy2.invert(e12, phi12))
m1 = int(pow(c11, d11, n11))
m2 = int(pow(c12, d12, n12))
print('m1 =', m1)
print('m2 =',m2)

D3原题，利用m1、m2,求解出b

构造求t

n2=209798341155088334158217087474227805455138848036904381404809759100627849272231840321985747935471287990313456209656625928356468120896887536235496490078123448217785939608443507649096688546074968476040552137270080120417769906047001451239544719039212180059396791491281787790213953488743488306241516010351179070869410418232801398578982244984544906579574766534671056023774009163991804748763929626213884208260660722705479782932001102089367261720194650874553305179520889083170973755913964440175393646890791491057655226024046525748177999422035469428780228224800114202385209306803288475439775037067014297973202621118959024226798935588827359265962780792266516120013602384766460619793738405476219362508944225007365127768741191310079985425349292613888185378948854602285379329682053663283534930182589905986063348509703027498270111412063194971956202729807710253369312175636837558252924035002153389909587349043986253518050303628071319876207392440085675892353421232158925122721273720564784886530611286461575045181073744696415657043278123662980166364494583141297996445429477446442693717498789391918530672770193730629928408766563592081857706608049076318165712479742423149330311238462044666384622153280310696667586565906758451118241914402257039981388209
m1 = 167033559384298522723574512241709447697750495062051373339874928117760768631565225663704494711294488556402223152830158600944819657473430506318731286655519728589208977191031849602792050411662024383502548579402516538753112670329781366297260905517214408459895097308286783418547254449419676568096534767340832822470233461516097690657337287889405321592527860524201824371955082411119548743528220794151774190322092515459637969925138496615421690273925560390321721643556915400569894100488394008220811596560968566833296068500476868375996187754631888256419438775013308064639754700359028260289266420692324376220460340153811660590804281527733243177527178698523018103373311259548716062006020121615186595491453534952848570829485638553678760994354019044715078062414748269425818079274218450448217803229617020494546843594180682307375768323235309661628678546003718924902228908888185484412626429441196588985691713767554591991735686919964937441820738008046218954331990752603146125777571183543616375946363623251491371247594696767767918341279655251868517380267258878990871525012299220182939441091806206624720194246691865367941280852353547267930167542329486261552854451001546455904682702366584763940463481732752992487773878685793275652314513014646439770319249
m2 = 69076592619651589706691933313826601279528159013379300261609967352748175972662567592943146333144902972780621576811778115958019397062270814057821407036352529372113467206560849267275602453288227390740346959857322649956992529510338912182696854496200041245775322561359546062736323363354733510660780489558215103581313753430117471361013972291126160134685745917715386613876414886325025010348396410346222272648657374977901786530969589123771261040601627906959627351426881111464943086191212001374558078570830214670111422731410682212770683631011038163623234630601007231955235905528750031898751733232446644402069580930596404887288935724879795199659228145390574503341087565153744389617539607111733080406125228559950446336384154674927952991964565965760896308198785777527690939982523416579778957846249005801121682470447753074839399698315364445972142571727376297422736232659133510385808957304351692629177239808890209690661982628408419571131470406142532800330250274534615063537773403062635865734585850821677880659194795963303700015814615804751909674946908768425855361277478190640780518117596780808975720826484146074528564147729911624750510271539697935538038871993380673492022099183863825435237650082706168588306816635866830411481021066926833372846305
PR.<x>=PolynomialRing(Zmod(n2))
f=m1*m2*x-(m1-m2)
f=f.monic()
root=f.small_roots(X=2^1020,beta=0.75,epsilon=0.05)
print(m1*m2*root[0]-(m1-m2))

求解b

t = 94476976265265641827602787049249578492995679429716482046924585940246717457042128023800961434763929914742777719081255795138910954579084380749185583907719246149786618272211075994958101199030515457710810020181711265592718382667417835300679818744556105115902732286571824909924263204098499659317182826854298624775226087960511390966633903776665957086981333664844689954842707299894825527456102357684702900215434762429187279846489983456835800865530440829770728920365517042040572671792205541796259443970816953362137707904728291364281547203770794228054266700322774140643180698948123359117635130447640013942149356692767628491724984585700056921275495622566239919234287223704276388600436608812344828297066467500081684211035484782425572477556398064326931308339522349977262739523525944259951551890257298499759018431685152074240475658756118917712727505720626269640871829914445489979998332574614114421748041115113139535028549083113148306447248881972052070543270343820033948146464079219887051369367284719845962861332344027439802931407999111600574151149695061790549599074232184205241527154267728361392434234918849232230207250936768141824533338058506493444626181620405061810567945382578748509014556142139898554833285230952931366575374187051795954535997
n2 = 209798341155088334158217087474227805455138848036904381404809759100627849272231840321985747935471287990313456209656625928356468120896887536235496490078123448217785939608443507649096688546074968476040552137270080120417769906047001451239544719039212180059396791491281787790213953488743488306241516010351179070869410418232801398578982244984544906579574766534671056023774009163991804748763929626213884208260660722705479782932001102089367261720194650874553305179520889083170973755913964440175393646890791491057655226024046525748177999422035469428780228224800114202385209306803288475439775037067014297973202621118959024226798935588827359265962780792266516120013602384766460619793738405476219362508944225007365127768741191310079985425349292613888185378948854602285379329682053663283534930182589905986063348509703027498270111412063194971956202729807710253369312175636837558252924035002153389909587349043986253518050303628071319876207392440085675892353421232158925122721273720564784886530611286461575045181073744696415657043278123662980166364494583141297996445429477446442693717498789391918530672770193730629928408766563592081857706608049076318165712479742423149330311238462044666384622153280310696667586565906758451118241914402257039981388209
m1 = 167033559384298522723574512241709447697750495062051373339874928117760768631565225663704494711294488556402223152830158600944819657473430506318731286655519728589208977191031849602792050411662024383502548579402516538753112670329781366297260905517214408459895097308286783418547254449419676568096534767340832822470233461516097690657337287889405321592527860524201824371955082411119548743528220794151774190322092515459637969925138496615421690273925560390321721643556915400569894100488394008220811596560968566833296068500476868375996187754631888256419438775013308064639754700359028260289266420692324376220460340153811660590804281527733243177527178698523018103373311259548716062006020121615186595491453534952848570829485638553678760994354019044715078062414748269425818079274218450448217803229617020494546843594180682307375768323235309661628678546003718924902228908888185484412626429441196588985691713767554591991735686919964937441820738008046218954331990752603146125777571183543616375946363623251491371247594696767767918341279655251868517380267258878990871525012299220182939441091806206624720194246691865367941280852353547267930167542329486261552854451001546455904682702366584763940463481732752992487773878685793275652314513014646439770319249
m2 = 69076592619651589706691933313826601279528159013379300261609967352748175972662567592943146333144902972780621576811778115958019397062270814057821407036352529372113467206560849267275602453288227390740346959857322649956992529510338912182696854496200041245775322561359546062736323363354733510660780489558215103581313753430117471361013972291126160134685745917715386613876414886325025010348396410346222272648657374977901786530969589123771261040601627906959627351426881111464943086191212001374558078570830214670111422731410682212770683631011038163623234630601007231955235905528750031898751733232446644402069580930596404887288935724879795199659228145390574503341087565153744389617539607111733080406125228559950446336384154674927952991964565965760896308198785777527690939982523416579778957846249005801121682470447753074839399698315364445972142571727376297422736232659133510385808957304351692629177239808890209690661982628408419571131470406142532800330250274534615063537773403062635865734585850821677880659194795963303700015814615804751909674946908768425855361277478190640780518117596780808975720826484146074528564147729911624750510271539697935538038871993380673492022099183863825435237650082706168588306816635866830411481021066926833372846305
c2=18352572608055902550350386950073774530453857897248738030380007830701135570310622004368605208336922266513238134127496822199799761713782366178177809597137102612444147565578155260524747439899150012223027218489946124086276814899675563837669559795153349686434242738207425653079514376089070980797596457151965772460109519623572502109592612394316680202287712465721767341302234806130244551387296133051760893033194962691942040228545508895009195291106297581470066545991352668826197346830561010198417527057944507902143965634058848276017283478933675052993657822322866778994956205033704582047618324071045349072526540250707463112668579342537349567247810715604220690215313641329522674080146047291570752430231923566302463491877377617044768978997438596643458475128936850994934029476030136643053997549253792076260765459166618369864942681056864815996253315631930002738854235841120321870075261782250357506436825550088826469396508045912258303652912217151127280959435741419961721418428605515096160344688795655562889755165362006775317188009008288782691705879510655892181975003485714604340542378477388225736316682379616676770234557939471098919647053799313777248678455620231721202780830980063824003076308811540534492317719811588898727134190545533822501681653
e2=65537
p2=gmpy2.iroot(gmpy2.gcd(t,n2),6)[0]
q2=n2//(p2**7)
r = 7
phi2 = (p2**(r-1))*(p2-1)*(q2-1)
d2 = int(gmpy2.invert(e2, phi2))
b = int(pow(c2,d2,n2))
print(b)

coppersmith求解出a，利用a、b、e3求出kphi，解出flag

求解a

b = 17623328397444755087284107444487160871617682792372566887446834913712379373851213638071138745775127796589871734472781755930251379295485892067473329763997583502625804363418069062645997342172778252731889437
e =464117832584849256876245026858584166064013216027422756825795521498385205721033353513543618744373301203834470328759823648931860535796880222946332534013897265901185999170322696957199889753713456154697105417293751933841379534096463865819008983795657599018683644132673713309334758819574886354704377483001339445757386992879690723631576273460553131155155316952245089907130766287714080403627930928130784991277544248116386917402984270528525775247134214492560997905367291867183866607941929214468777104690392820823035675612092617083295882759857152154377282721152947480472621698324590869278751145403323940075314010289498908873588009861230984997557274773415874956453307178971675014333345657736750118816545969164208900208803031938469633040195998941962960862469507517241931009534811253696410851868499055867913530737331005151134014871819905410958792932531597274862405076661694656088513465559617186646712502574197476333665637476068284511221311807581941866208929989854046731148928578091744976377612425409987679627546723108095722115773079517077535943913527056273328898166164977293075443526474958962783904307031337910198587916917973655637855317764238521650195864421643538425185311500988998567302569476110003110592320332553740947779735694862664952369085
n =539779851369541956878655738599584730199799866957191805784596190682932284216781781433367450841202917758999300635019369629627621029957135109806205877317954671312041249493462048283611940752235036153024920172209763260723728345918562258401803973624430150143563078517485996070862532682695228590709019451174548520135142052216785774589096706631010293690859363524584240662502290912412366366114571976050857239915691266377257797199583543940504695517331512813468837128344612227973709974625418257243011036826241599265375741977853552204640800449679679351666009764297016524814036295707311913711955324055690490892097177271718850857268982130811714517356073266905474635370690445031512184247179039751734276906533177939993769044135143389748416635981226449566039039202521305851567296884751935162651063209779647359922622084851547605090230221057349511482738300221222563908357379545905837110168948295030747460300104202323692732549831403834387939156877086852393515817984772384147449841124275061609701453997579569931391166586163299940486204581696722731952467570857217406030804590055255431828403195798003509083922294733709507134156466158642941338493323430671502043066148246348074878064089651235355282144209668143249348243220714471988019011613749340243917652821
P.<x> = PolynomialRing(Zmod(n))
f=x*e-b
f=f.monic()
roots=f.small_roots(X = 2^1400,beta = 0.1)[0]
a=roots//b
print(a)

求解flag

import gmpy2
import libnum
from gmpy2 import *
b = 17623328397444755087284107444487160871617682792372566887446834913712379373851213638071138745775127796589871734472781755930251379295485892067473329763997583502625804363418069062645997342172778252731889437
a = 16731588253866128571163910758846497670928988943944436618514118121761227689113110943465936457030051710610254169629932203082368465978112219532158626669990117160986135699541953274434781877420432743573801621
r = 7
e3=8179300978753084587812861894047395225516049110376948812109811319430275614612773726672345893359691900281432484382670047044697374818043512731533402576374645405477207239801498428774783768163880078495448747421425078521981578408638790336528372019271073712013371141939808017049399434858687299480461753638164719404612128939787055797762174745092074547412183349192156638711750872083313795551439465507724807626674514935170104573715458782366469587138508845980490673890245713729782917089910271980557159592807350504157192913530007199510144004848020221181558472160543018733124225266127379373751910439604459368078652499029070936707349862139053913745186413782066470461478961703013591655136140060879250067379283913798867648758171004535775565306842444545755351202796833177560656564652632975685912935281581268141803696686952259539945588609591385807620108279333498170028167338690235117003515264281843953984997958878272347778561933726792473981855755454522886321669676790813189668084373153897754540290867346751033567500922477317530445967753955221454744946208555394588111484610700789566547507402309549957740815535069057837915204852490930168843605732632328017129154852857227895362549146737618906180651623216848500491438142456250653458053922622240299736136335179639180898730269690699965799644757774472147210271111150769048976871249731156387939260749192370361488285775377622944817570292095201906142567403539151179209316853493906909989301225903409448461436855145
n3=539779851369541956878655738599584730199799866957191805784596190682932284216781781433367450841202917758999300635019369629627621029957135109806205877317954671312041249493462048283611940752235036153024920172209763260723728345918562258401803973624430150143563078517485996070862532682695228590709019451174548520135142052216785774589096706631010293690859363524584240662502290912412366366114571976050857239915691266377257797199583543940504695517331512813468837128344612227973709974625418257243011036826241599265375741977853552204640800449679679351666009764297016524814036295707311913711955324055690490892097177271718850857268982130811714517356073266905474635370690445031512184247179039751734276906533177939993769044135143389748416635981226449566039039202521305851567296884751935162651063209779647359922622084851547605090230221057349511482738300221222563908357379545905837110168948295030747460300104202323692732549831403834387939156877086852393515817984772384147449841124275061609701453997579569931391166586163299940486204581696722731952467570857217406030804590055255431828403195798003509083922294733709507134156466158642941338493323430671502043066148246348074878064089651235355282144209668143249348243220714471988019011613749340243917652821
c3=113097822337683973761068913398570777162211043704088253732500045618770280334319497174908657828372816818344430304314992760410247741225285170975119344962728883084314382093407445567724674775086423808679124143380073906159023182353116556175251427048715466914368972746661938211846262612414049036821553068430149530397389927209475908905748728402722287875974303298260579839357610962198145974153609818939841880084892796820949226354126424023144300953584658958900737493704530725894948802258740332090822797815745616247879170037794873059391625680745994045522420168248552864215035136318711240256011217929372430302003068882829637056296413462078222453765071094277727760527662423010417144554652783429899139309180017349156600053882338180319473460877576898373222480215735280046214925463242092830060830764299787309912687294672319845054775281463150375545716818434962456139485501224661520991156961587158843064393883274763714930309353593180897123378717852182761518709151878662808890356934477932099818218743384674756674800089177733447066489275506387382342429495897972218764782517198727316942685748481956118012927027254979181519862451112593068440686462293151078537886822555211870303467014484443432209106264020502334805536091587252238173816637270028678636848763
phi3 = (e3//b)*a - 1
d3 = gmpy2.invert(e3, phi3)
m = int(pow(c3, d3, n3))
print(libnum.n2s(m))
# b'qwb{8633ce6d-fece-4cf1-8f0f-f27e5bf6d678}'

qwb{8633ce6d-fece-4cf1-8f0f-f27e5bf6d678}

结语

已经到能力上限了，最后两道一道五解、一道两解再给两天估计也做不出。

遗憾未出线😢

又为什么总在遗憾呢？

Harry's Blog

2022强网杯·Crypto

强网先锋

ASR

题目

题解

polydiv

题目

题解

Crypto

myJWT

题目

题解

Factor

题目

题解

结语