babysign
题目
1 | import hashlib |
题解
ecdsa签名,k泄漏,有msg算其hash值,可求私钥x
$x \equiv r^{-1}(ks-H(m)) \bmod n$
1 | import hashlib |
DASCTF{11b7311d4f0137074a7256d3eb82f368}
NTRURSA
题目
1 | from Crypto.Util.number import * |
题解
- 多项式RSA解出h
- 对于NTRU参数,用LLL求g1
- 遍历rand异或出n的因子g
- 常规RSA求解出flag
1 | # sage |
DASCTF{P01yn0m141RS4_W17h_NTRU}
easyNTRU
题目
easyNTRU
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81from Crypto.Hash import SHA3_256
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from secret import flag
# parameters
N = 10
p = 3
q = 512
d = 3
assert q>(6*d+1)*p
R.<x> = ZZ[]
#d1 1s and #d2 -1s
def T(d1, d2):
assert N >= d1+d2
s = [1]*d1 + [-1]*d2 + [0]*(N-d1-d2)
shuffle(s)
return R(s)
def invertModPrime(f, p):
Rp = R.change_ring(Integers(p)).quotient(x^N-1)
return R(lift(1 / Rp(f)))
def convolution(f, g):
return (f*g) % (x^N-1)
def liftMod(f, q):
g = list(((f[i] + q//2) % q) - q//2 for i in range(N))
return R(g)
def polyMod(f, q):
g = [f[i]%q for i in range(N)]
return R(g)
def invertModPow2(f, q):
assert q.is_power_of(2)
g = invertModPrime(f,2)
while True:
r = liftMod(convolution(g,f),q)
if r == 1: return g
g = liftMod(convolution(g,2 - r),q)
def genMessage():
result = list(randrange(p) - 1 for j in range(N))
return R(result)
def genKey():
while True:
try:
f = T(d+1, d)
g = T(d, d)
Fp = polyMod(invertModPrime(f, p), p)
Fq = polyMod(invertModPow2(f, q), q)
break
except:
continue
h = polyMod(convolution(Fq, g), q)
return h, (f, g)
def encrypt(m, h):
e = liftMod(p*convolution(h, T(d, d)) + m, q)
return e
# Step 1
h, secret = genKey()
m = genMessage()
e = encrypt(m, h)
print('h = %s' % h)
print('e = %s' % e)
# Step 2
sha3 = SHA3_256.new()
sha3.update(bytes(str(m).encode('utf-8')))
key = sha3.digest()
cypher = AES.new(key, AES.MODE_ECB)
c = cypher.encrypt(pad(flag, 32))
print('c = %s' % c)out
1
2
3h = 39*x^9 + 60*x^8 + 349*x^7 + 268*x^6 + 144*x^5 + 469*x^4 + 449*x^3 + 165*x^2 + 248*x + 369
e = -144*x^9 - 200*x^8 - 8*x^7 + 248*x^6 + 85*x^5 + 102*x^4 + 167*x^3 + 30*x^2 - 203*x - 78
c = b'\xb9W\x8c\x8b\x0cG\xde\x7fl\xf7\x03\xbb9m\x0c\xc4L\xfe\xe9Q\xad\xfd\xda!\x1a\xea@}U\x9ay4\x8a\xe3y\xdf\xd5BV\xa7\x06\xf9\x08\x96="f\xc1\x1b\xd7\xdb\xc1j\x82F\x0b\x16\x06\xbcJMB\xc8\x80'
题解
赛时,Mu_chen师傅负责这道,出了,我便也没看了。
以后为赛后复现。
关注以下代码
1 | p = 3 |
发现作为AES加密的密钥,长度为10的m,每个值只有-1、1、0三种可能
可以爆破求解
1 | from itertools import product |
DASCTF{b437acf4-aaf8-4f8f-ad84-5b1824f5af9c}
lwe?
题目
lwe
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32from secret import secret
assert len(secret)==66*3
sec = [ord(x) for x in secret]
DEBUG = False
m = 66
n = 200
p = 3
q = 2^20
def errorV():
return vector(ZZ, [1 - randrange(p) for _ in range(n)])
def matrixMn():
return matrix(ZZ, [[q//2 - randrange(q) for _ in range(n)] for _ in range(m)])
A, B, C = matrixMn(), matrixMn(), matrixMn()
x = vector(ZZ, sec[0:m])
y = vector(ZZ, sec[m:2*m])
z = vector(ZZ, sec[2*m:3*m])
e = errorV()
b = x*A+y*B+z*C+e
if DEBUG:
print('x = %s' % x)
print('y = %s' % y)
print('z = %s' % z)
print('e = %s' % e)
print('A = \n%s' % A)
print('B = \n%s' % B)
print('C = \n%s' % C)
print('b = %s' % b)
题解
读取好数据
将out文件里的双空格全替换改为了单空格,才写的代码
将x、y、z横着堆叠成$1×198$的矩阵,将A、B、C竖着堆叠成$198×200$的矩阵,发现是GGH
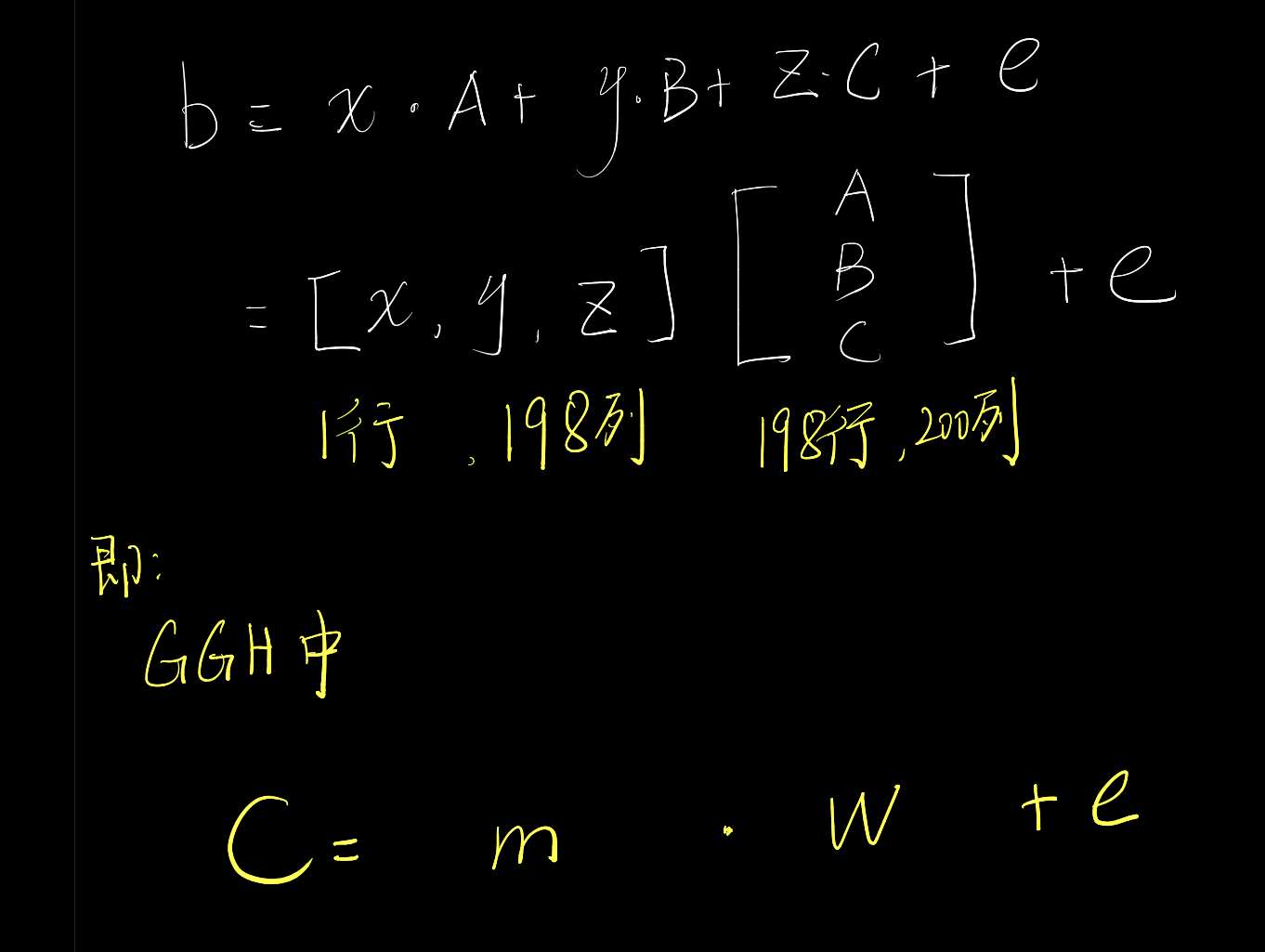
搜到babai的方法(并不是最优解,跑了快十分钟)可忽略e,求出明文
https://www.bnessy.com/archives/long-yuan-zhan--yi-2021writeup
按照uuid的格式拼写好flag
1 | from sage.modules.free_module_integer import IntegerLattice |
1 | m = ['O', 'h', ',', ' ', 'y', 'o', 'u', ' ', 'g', 'e', 't', ' ', 'i', 't', '?', '?', ' ', 'H', 'e', 'r', 'e', ' ', 'i', 's', ' ', 't', 'h', 'e', ' ', 'f', 'l', 'a', 'g', ':', ' ', "'", 'D', 'A', 'S', 'C', 'T', 'F', '{', 'u', 'u', 'i', 'd', '}', "'", '.', ' ', 'W', 'h', 'a', 't', '?', ' ', 'Y', 'o', 'u', ' ', 'd', 'o', 'n', "'", 't', ' ', 'k', 'n', 'o', 'w', ' ', 't', 'h', 'e', ' ', 'u', 'u', 'i', 'd', '?', ' ', 'T', 'h', 'e', ' ', 'f', 'i', 'r', 's', 't', ' ', 'p', 'a', 'r', 't', ' ', 'i', 's', ' ', "'", 'd', 'c', 'f', '4', '1', '5', '5', '6', "'", ',', ' ', 's', 'e', 'c', 'o', 'n', 'd', ' ', 'p', 'a', 'r', 't', '-', '>', ' ', "'", 'c', '1', '9', '4', "'", ',', ' ', 'a', 'n', 'd', ' ', 't', 'h', 'e', 'n', ' ', "'", '4', 'c', '6', '6', "'", ',', ' ', "'", '9', '0', '9', '2', "'", '.', ' ', 'A', 'n', 'd', ' ', 'f', 'i', 'n', 'a', 'l', 'l', 'y', ',', ' ', 'i', 't', "'", 's', ' ', "'", '0', '5', '9', 'e', '0', 'b', 'f', '8', 'b', '8', '4', 'e', "'", '!', '!', '!', ' ', '0', 'v', '0'] |
DASCTF{dcf41556-c194-4c66-9092-059e0bf8b84e}