背包问题

背包加密基于背包问题。

而背包问题，是指设有一个可以载重S的背包，在有 n 个重量分别为 a1,a2,…,an的物品情况下，如何在不重复选择的前提下将物品装入背包且正好使其满载的问题。

数学表述如下：
$$
x_1a_1+x_2a_2+···+x_na_n=S, x_i \in (0,1),a_i>0
$$
实际上，我们可以将明文转换成数字，并将其二进制01码从高位到低位依次作$x_i$.

公布$a_i$、$S$这样就实现了,利用背包问题来简单加密明文。

此时，若要破解出$x_i$,爆破攻击的时间复杂度是$O(2^n)$，非常困难也非常安全，但没有意义。

因为加密的目的，是让指定的人（同时有公私钥的人）能快速解密，而只有公钥的人则无法快速解密。

如上所述的加密方式，没有这么一种「私钥」能让拥有者快速解出明文$x_i$

超递增序列

在讲改进后基于背包问题的背包加密之前，先谈谈超递增序列。

上文说到「若要破解出$x_i$,爆破攻击的时间复杂度是$O(2^n)$，非常困难」，那么，是否有特殊情况可以快速求出序列X(即$x_i$组成的数列)呢？

答案是：有。

这里讲的超递增序列即是。

超递增序列是每一个元素都大于或等于之前所有元素之和的序列，即：
$$
r_i ≥ r_1 + r_2 + r_3 + ··· + r_{i-1}
$$
也即:
$$
r_i ≥ 2 •r_{i-1}
$$

当明文与超递增序列依次相乘再求和时
$$
x_1r_1+x_2r_2+···+x_nr_n=S, x_i \in (0,1),r_i>0
$$
我们可以通过依次比较S与序列中最大的元素大小关系，来确定该元素性质。

例如，若$S > r_n$,则$r_n$必然存在于等式左边，即$x_n=1$

因为哪怕小于$r_n$的所有元素都存在于等式左边，它们的和也小于$r_n$.所以$S$若要大于$r_n$，$r_n$就必须存在。

接下来，令$S = S - r_n$，再比较$S$与$r_{n-1}$，同理可得$x_{n-1}$

循环以上步骤，直到确定序列$X$所有元素。

如此一来，我们知道若用超递增序列加密明文，是非常容易可破解出明文的。

背包加密

1977年，Merkle与Hellman合作设计了背包加密算法，该算法提出后密码学界提出了很多背包型加密算法。

正如前文所言，背包问题显然不是一个加密体系，若加密所用序列并不特殊，求$x_i$对所有人都很困难。

于是Merkle–Hellman背包加密算法诞生，其流程如下

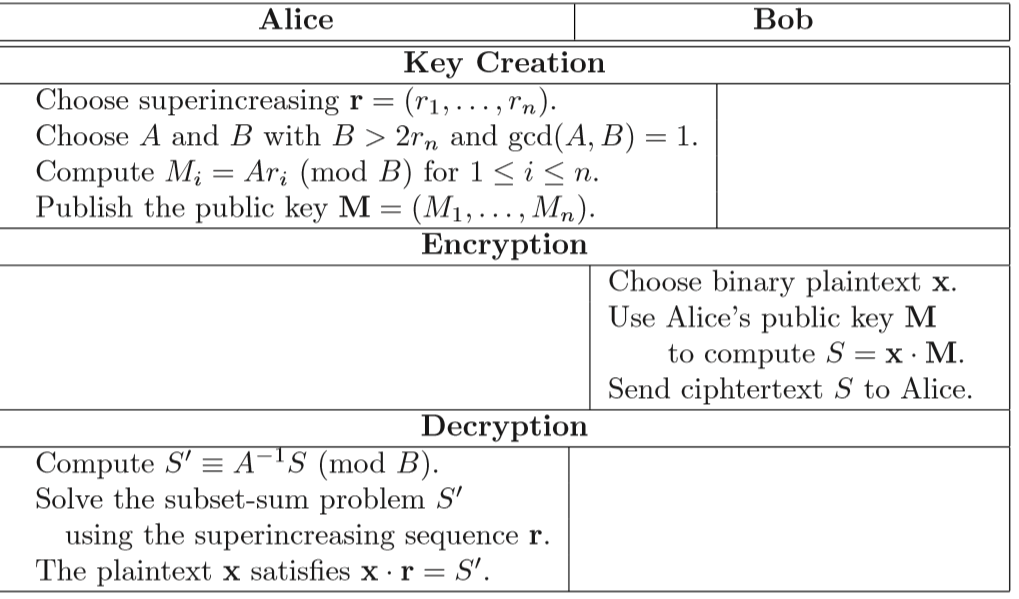
加密

明文
- 明文字符串转数字
- 明文数字转二进制
- 生成明文序列$x=(x_1,x_2,x_3,···,x_n), x_i \in (0,1)$
  
  $x_i$为明文数字二进制下每一位
私钥

生成超递增序列$r=(r_1,r_2,r_3,···,r_n)$做私钥序列
公钥
- 生成模数B，满足$B>\sum\limits_{i=1}^{n}a_i$, 即$B>2r_n$
- 生成乘数A，满足$gcd(A,B)=1$
- 生成公钥序列$M=(M_1,M_2,M_3,···,M_n)$，其中$M_i ≡ Ar_i \mod B$
密文

生成密文$S = x•M = \sum \limits_{i=1}^{n}x_iM_i$

公布序列M, 乘数A, 模数B, 密文S

解密

计算A关于模B的逆元$A^{-1}$
计算$S’ \equiv A^{-1}S \equiv A^{-1}\sum_{i=1}^{n}x_iM_i\equiv A^{-1}\sum_{i=1}^{n}x_iAr_i\equiv \sum_{i=1}^{n}x_ir_i \mod B$
利用超递增序列$r$的性质，求解出明文二进制
明文二进制转数字，再转字符串

如上流程，公、私钥拥有者可以计算出$S’$，然后利用超递增序列$r$轻易求解出明文

仅有公钥者，计算出$S’$后，因为没有序列$r$便无法利用超递增序列的性质求解

只能看向这个等式
$$
S = x•M = \sum \limits_{i=1}^{n}x_iM_i
$$
而若正常选择好乘数$A$、序列$r$，模B后的序列$M$各元素（$M_i ≡ Ar_i \mod B$）将丧失原大小顺序性质。

换言之，攻击者将面临的是上文中背包问题里复杂度为$O(2^n)$的难题，这保障了背包加密的安全性。

但近些年来，自从有关LLL的论文发表后，基于背包的密码系统出现了致命的漏洞。

攻击

参数不当

正如前文所讲，若乘数$A$、序列$r$大小不当则可能使得乘积过小，即：$Ar_i \mod B = Ar_i$

那么公钥序列$M$就是肉眼可见的超递增序列了，直接利用性质可求出明文。

背包问题通解

当密度$d = \cfrac{len(M)}{\log_2(max(M_i))}<0.9408$时，LLL算法能通杀这类背包问题。

用公钥序列$M=(M_1,M_2,M_3,···,M_n)$、密文S构造格子
$$
\left(\begin {array}{c} x_1 \newline \vdots \newline x_{n-1} \newline x_n \newline 0 \end{array} \right) <=>\left(\begin {array}{c} 1 & 0 & \cdots & 0 & M_1 \newline 0 & 1 & \cdots & 0 & M_2 \newline \vdots & \vdots & \ddots & \vdots & \vdots \newline 0 & 0 & \cdots & 1 & M_n \newline 0 & 0 & \cdots & 0 & S \end{array} \right)
$$
用LLL求右边格子的最短正交基，即为左边的明文$x$

# Sage
import libnum
M = []
S = 
n = len(M)
Mat = Matrix.identity(n)

last_row = [0 for x in M]
M_last_row = Matrix(ZZ, 1, len(last_row), last_row)

last_col = M[:]
last_col.append(S)
M_last_col = Matrix(ZZ, len(last_col), 1, last_col)

Mat = Mat.stack(M_last_row)
Mat = Mat.augment(M_last_col)

X = Mat.LLL()
# print(X)
for t in X:
    tmp = t[:-1]
    ans = [str(abs(k)) for k in tmp]
    try:
        flag = int(''.join(ans), 2)
        print(libnum.n2s(flag))
    except:
        pass
print('0ver')

进一步原理，详见参考[2]&[3]

子集积问题

以上所述的背包问题也叫子集和问题，即：关于子集的和的问题。

子集积问题，想办法退化为子集和问题即可解。

详见参考[3]

参考

[1] https://ctf-wiki.org/crypto/asymmetric/knapsack/knapsack/

[2] https://lazzzaro.github.io/2020/05/13/crypto-其他加密算法/#Merkle-Hellman背包加密（Knapsack）

[3] https://jayxv.github.io/2020/06/08/密码学学习笔记之knapsack/

Harry's Blog

CTF·背包问题相关