寒假修炼记（一）

序言

哈尔滨地区的大学，寒假早而久。
于12.27日十点便已解放，28日下午七时方才到家。

🤔大有效仿凡人修仙转之意，本着记录每日以“匕首反握，杀死懒惰”原则，开下此篇。

大体上，密码手的安排，自然是得先把密码搞清楚有多难。

又因为谋划着转到计科，还得学些C、离散数学与做些玩具般的项目为好。

12.28/29

TCP/IP

王小波

愁容骑士

乌云典当铺

酒精

计算器乐

炉石传说

---

12.30

Crypto·RSA

RSA系列视频：风二西RSA教学

数学知识–模运算

基本运算

(a + b) % p = (a % p + b % p) % p
(a - b) % p = (a % p - b % p) % p
(a * b) % p = (a % p * b % p) % p
a ^ b % p = ((a % p) ^ b) % p

注：% 为取余， ^为幂.

结合律

((a + b) % p + c) = (a + (b + c) % p) % p
((a * b) % p * c) = (a * (b * c) % p) % p

交换律

(a + b) % p = (b + a) % p
(a * b) % p = (b * a) % p

分配律

(a + b) % p = (a % p + b % p) % p
((a + b) % p * c) % p = ((a * c) % p + (b * c) % p )%p

重要定理

若 a ≡ b (mod p)，则对于任意的 c，都有(a + c) ≡ (b + c) (mod p)
若 a ≡ b (mod p)，则对于任意的 c，都有(a * c) ≡ (b * c) (mod p)
若 a ≡ b (mod p)，c ≡ d (mod p)，则
(a + c) ≡ (b + d) (mod p)
(a - c) ≡ (b - d) (mod p)
(a * c) ≡ (b * d) (mod p)
(a / c) ≡ (b / d) (mod p)

原理证明

证明RSA加/解密的正确性

py库libnum

获得指定比特位素数

libnum.generate_prime(bits) 

字符串与数字之间的转换（string to num

libnum.s2n(m)

求解逆元

libnum.invmod(e, phi) 

费马分解

当直接分解n不出且知道p、q两素数大小接近时，可以用费马分解写脚本来得到p、q

代码

def isqrt(n):
  x = n
  y = (x + n // x) // 2
  while y < x:
    x = y
    y = (x + n // x) // 2
  return x

def fermat(n, verbose=True):
    a = isqrt(n) # int(ceil(n**0.5))
    b2 = a*a - n
    b = isqrt(n) # int(b2**0.5)
    count = 0
    while b*b != b2:
        a = a + 1
        b2 = a*a - n
        b = isqrt(b2) # int(b2**0.5)
        count += 1
    p=a+b
    q=a-b
    assert n == p * q
    return p, q
fermat(n) 

公/私钥

公钥生成

from Crypto.PublicKey import RSA
rsa_components = (int(n), int(e))  # 只需要n，e
keypair = RSA.construct(rsa_components)
with open('pubckey.pem', 'wb') as f :
    f.write(keypair.exportKey()) 

私钥生成

from Crypto.PublicKey import RSA
rsa_components = (int(n),int(e),int(d),int(p),int(q))  # 至少需要n、e、d
keypair = RSA.construct(rsa_components)
with open('private1.pem', 'wb') as f :
    f.write(keypair.exportKey()) 

公钥读取

from Crypto.PublicKey import RSA
with open("pubckey.pem","rb") as f:
    key = RSA.import_key(f.read())
    print('n = %d' % key.n)
    print('e = %d' % key.e) 

私钥读取

from Crypto.PublicKey import RSA
with open("private1.pem", "rb") as f:
		key = RSA.import_key(f.read())
		print('n = %d' % key.n)
    print('e = %d' % key.e) 
    print('d = %d' % key.d)
    print('p = %d' % key.p) 
    print('q = %d' % key.q)

OAEP

最优非对称加密填充（英语：Optimal Asymmetric Encryption Padding，缩写：OAEP

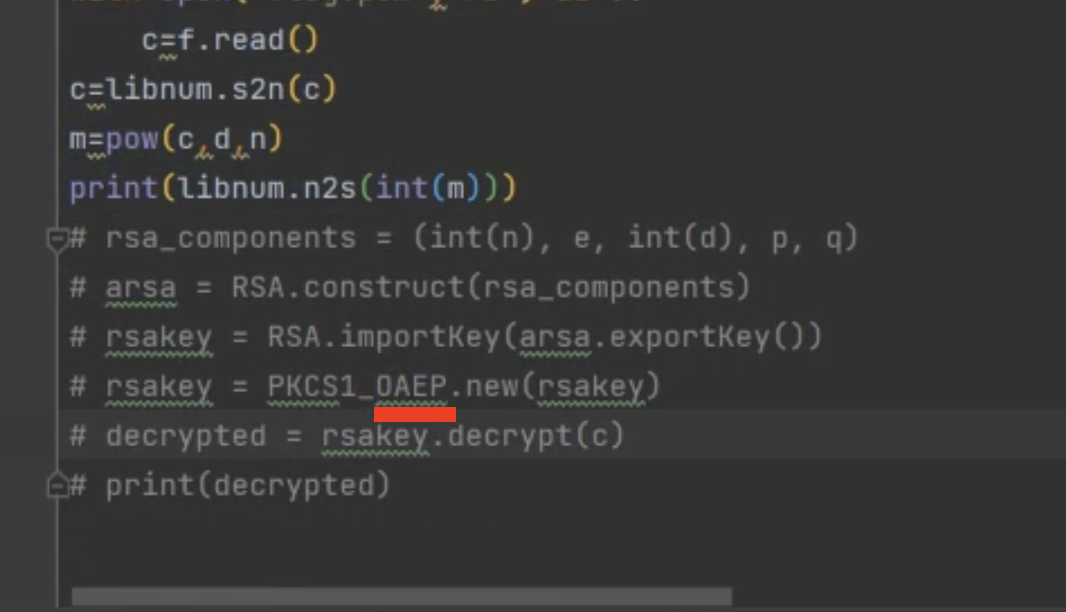
OAEP结构，正常读取求解会导致结果乱码。
需要针对性的代码

from Crypto.Cipher import PKCS1_v1_5
from Crypto import Random
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP


random_generator = Random.new().read
rsa = RSA.generate(2048, random_generator)
# 生成私钥
private_key = rsa.exportKey()
# print(private_key.decode('utf-8'))
with open('rsa_private_key.pem', 'wb')as f:
    f.write(private_key)
# 生成公钥
public_key = rsa.publickey().exportKey()
# print(public_key.decode('utf-8'))
with open('rsa_public_key.pem', 'wb')as f:
    f.write(public_key)


#测试用密钥加密
public_key = RSA.importKey(public_key)
msg='flag'
pk = PKCS1_v1_5.new(public_key)
encrypt_text = pk.encrypt(msg.encode())
print(encrypt_text)

#测试密钥解密
private_key = RSA.importKey(private_key)
pk = PKCS1_v1_5.new(private_key)
msg = pk.decrypt(encrypt_text,0)
print(msg)


#两种标准
rsa_components = (n, e, int(d), p, q)
arsa = RSA.construct(rsa_components)
rsakey = RSA.importKey(arsa.exportKey())
rsakey = PKCS1_OAEP.new(rsakey)
decrypted = rsakey.decrypt(c)
print(decrypted)

---

12.31

Crypto·RSA

共模攻击

针对同明文m、同n，且$e_1$与$e_2$互质

出题角度

对明文m用两个e，同一n加密。

格式：

m = ....
n1 = n2 = n = ...
e1 = ...
e2 = ...
c1 = ...
c2 = ...

解题角度

数学角度

学习了扩展欧几里得算法（先前用来算e对phi的逆元d）,

共模攻击也用上了

扩展欧几里得算法：对于不全为0的a、b,有：ax + by = gcd(a, b)
其中gcd(a, b) 表示 a，b的最大公约数

用其得到 满足 $s_1·e_1 + s_2·e_2 = gcd(e_1, e_2) = 1$的 $s_1、s_2$

最终，明文m可用如下公式得到：

$$m = (C_1^{s_1}modn\cdot C_2^{s_2}modn)modn$$

计算机角度

import gmpy2
import libnum
n= 25333966058003377512707481338795714713737652659944601834182685873529702913988641983855700459996104700470621411559153944988952210084014634675583566338568882440708528997808798650962116756969822211586531522430245040013570571043385238601846104615050089457836721437790715225367971106085839523500735480715155424498941150468093083816830215632716244390679417218873179734276657411907216486790815037105108306055794473002315541787461904728375164737225486501009857299717749346279371251245318729951905832578739696926931502225899707226264570557623527701806829827566904224572897378639191756878049342203546309520458672464170859577433
e1= 2333
c1= 11355981897781478907853356911752561659125575027336719997290835661089901154031171698660586203170528368228850895159361637188990782030255983633790580700032092629587631108597144196551438410868034739981960656110887650747325311613900008001234835897835613759692146419080113176963747835592656185435741504176116672174539018089139547795447109458469225330809064539216773123671814859510069089532677704482026169178543062578686794346026774853085101278125763460212801929360456888869350105294595904940799522522144740464043605342348269086324747729288399275079874271519208155039364092577755518532799345651172433227745483422620900776136
e2= 23333
c2= 1326499538902841116411674554069945581390130048432351353260154261863309471312810811160302458644816390944833633923435634961251092531893503039914793217247984595331920909367627316087404934402312358642315675486438968585084964845763881078835787872160374025547400141298650794551970291119975344578667689961134814676553190178139842507675899262024572370313939107080072875068218336255452161407859907308656094331557912187788276334833723893856310434523337557011032081467262457427167978528280339494077785813461280853735266463152709443731638714219391773144349752633555310299318290576258086971373777118482642702020599928071855133041

'''
# 没忍住，验证了下求逆元的函数用来解好不好使
# 因为都是用到扩展欧几里得原理，当然可解
s1 = int(gmpy2.invert(e1, e2))
s2 = int((1-e1*s1)/e2)
m = pow(c1, s1, n) * pow(c2, s2, n)% n
print(libnum.n2s(m))
# b'flag{6ed4c74e022cb18c8039e96de93aa9ce}'
'''

s, s1, s2 = gmpy2.gcdext(e1, e2)  # s为gcd(e1, e2)
m = int(pow(c1, s1, n)*pow(c2, s2, n)%n)
print(libnum.n2s(m))

原理证明

证明共模攻击的可行性

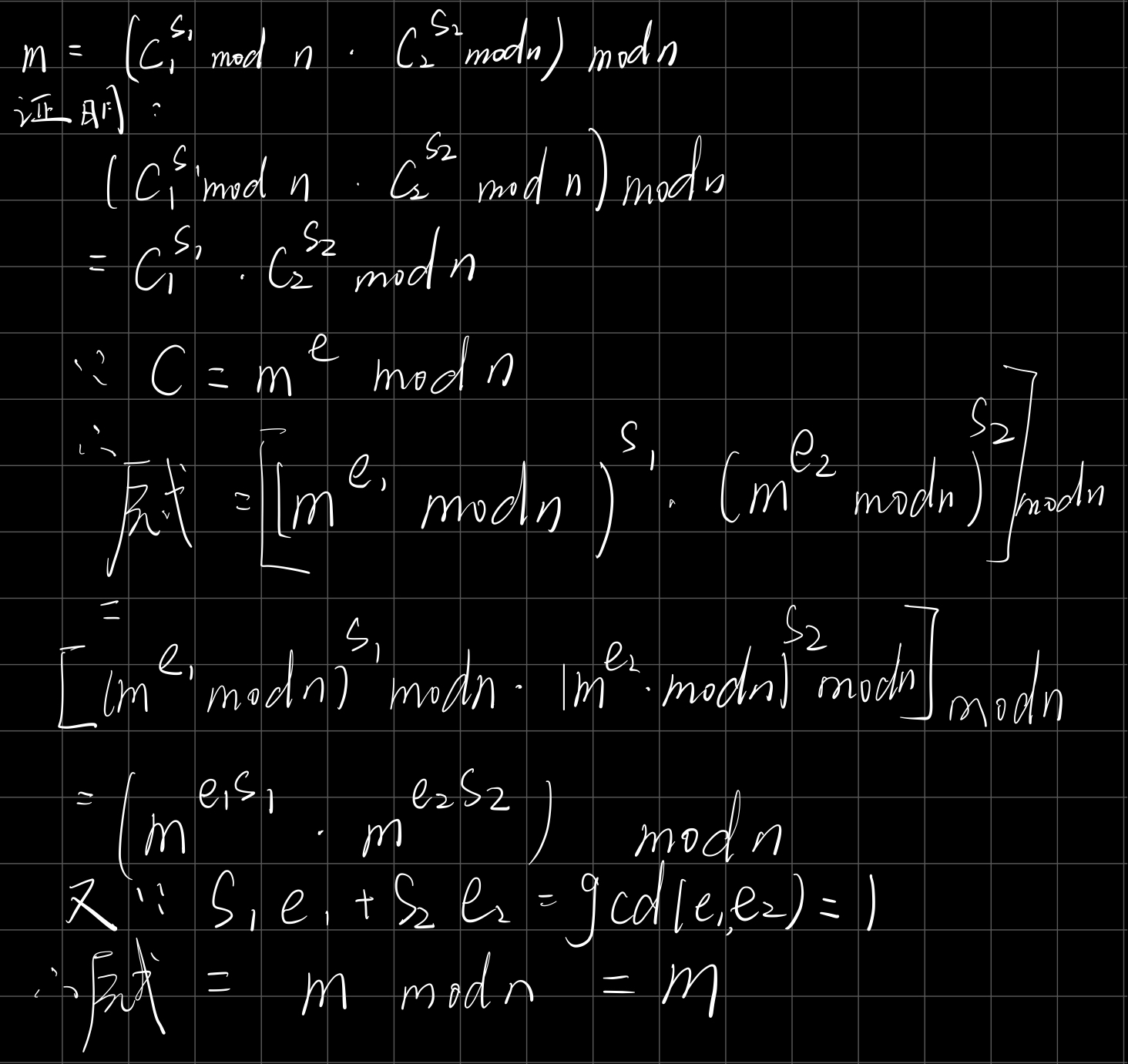
维纳攻击

针对e过大

原理🤔

道阻且长

代码

import gmpy2
import libnum

def continuedFra(x, y):
    """计算连分数
    :param x: 分子
    :param y: 分母
    :return: 连分数列表
    """
    cf = []
    while y:
        cf.append(x // y)
        x, y = y, x % y
    return cf
def gradualFra(cf):
    """计算传入列表最后的渐进分数
    :param cf: 连分数列表
    :return: 该列表最后的渐近分数
    """
    numerator = 0
    denominator = 1
    for x in cf[::-1]:
        # 这里的渐进分数分子分母要分开
        numerator, denominator = denominator, x * denominator + numerator
    return numerator, denominator
def solve_pq(a, b, c):
    """使用韦达定理解出pq，x^2−(p+q)∗x+pq=0
    :param a:x^2的系数
    :param b:x的系数
    :param c:pq
    :return:p，q
    """
    par = gmpy2.isqrt(b * b - 4 * a * c)
    return (-b + par) // (2 * a), (-b - par) // (2 * a)
def getGradualFra(cf):
    """计算列表所有的渐近分数
    :param cf: 连分数列表
    :return: 该列表所有的渐近分数
    """
    gf = []
    for i in range(1, len(cf) + 1):
        gf.append(gradualFra(cf[:i]))
    return gf


def wienerAttack(e, n):
    """
    :param e:
    :param n:
    :return: 私钥d
    """
    cf = continuedFra(e, n)
    gf = getGradualFra(cf)
    for d, k in gf:
        if k == 0: continue
        if (e * d - 1) % k != 0:
            continue
        phi = (e * d - 1) // k
        p, q = solve_pq(1, n - phi + 1, n)
        if p * q == n:
            return d


n= 68781015120012754009149819243839432182753699533745468739333557116438115901358573880902197723852823949505376140916570536753019491036629572363854637530919546688901226752085109196549145599781909847664046508960094447692268230516763088293911965638780888720788954194778424857089535187609738198309161969913567107861
e= 54093680529782962282616750547542407544796590039913570980901028264103594185617926725669901283009540557359666956131385125727959502505561517117179644650419753631214251337533961664493198676862110639584202010794500844074619335752668896589407110076134931918634061631574656816488381501901503924226166074238518619869
c= 30443384983816710270001651296607959522389400057103143909277631290995899073895621701281106228069835965181342091582584186637031613250922961166298411359757600825556083868477673357860585539016515776933117915504873987178857740106223631465737111746470236003857656528610755145017342412306680097140732745012583119076

d=wienerAttack(e, n)
m=pow(c, d, n)
print(libnum.n2s(m).decode())

低加密指数攻击

针对e极小的情况

原理

代码实现

import gmpy2
import libnum
"""
a,b = gmpy2.iroot(mm, e)
a 为 mm开e次方的结果，b为是否刚好开得出来（True/False）
"""

def de(c, e, n):
    k = 0
    while True:
        mm = c + n*k
        result, flag = gmpy2.iroot(mm, e)
        if True == flag:
            return result
        k += 1
n= 14067473525623615859223663589118945198091192669401088734569589535726733244095067264729942915265175903139441309376381225701454902095234966599914234681888481774607095853830772571665038109641511499155604914228117882196188074964226780922239011682486198651997912713999544628177959592818928976240251790858062449396082494272361535640237914373270152455829541596341184902017633404494979208958080467979235974182507427501682492000572071306960595992848840147393057648929439822116261337091431441205378542080755128597543738922210525692259529009107645032171097155449558362749512243918901171631681472217935131865121871798425854707759
e= 3
c= 2217344750798294937344050117513831761010547351781457575945714176628679412650463329423466955026804439931765627111856888102133234836914006818023839994342283023142702993182665344445325734299047409223354338948863171846780674244925724334091153701697864918695050507247415283070309

m=de(c,e,n)
print(m)
print(libnum.n2s(int(m)).decode())

低加密指数广播攻击

相同的m，e(小！素数)
不同的n、c

题目

e= 23
n= [13717717494437510618655695859379240545274880285465336084980383077735368449287887730112865484794564775965333130485171954220538624992093337243861524569409700886337014234713178570668109071829948370957268039331890309426003791637196331784060347281424746354933919606729084027951927846702619927770747545446918328438622383693133548955188836386005534760206952510151018682387718085250017581376063736842317438569821243548189241925924255433864969372030426408000285820602186583603693449295808074728161954043126958695722583028507474298960280230105785438240951800348819439737765386534993474369225493776777465563613151321621063835151, 16558144096449901801273741638840778818249738276674307459380900970606210353540178775588473225243101747716461656540937897967914169123169165285058141215885778524114034353669913224125616631533581720637295574241914527632355261186084856237825159147911418425949368185785914138348023296084922073326022172722255827572970855050651303634156974527741633815671696193750844008859783609126795877812454556337806158402992021810288807118117148245357511324959680345093491733679424737914086895189219675071776517106662608171511296158300059171152501359288000451820034267372848220853491805152939787676992158798075475571822718598861536277813, 17241243429631602964596121000369815061212483336345771502751354875235046514210996399502810866301956320705757581154321265449903125364826064459735361374900736506813626157686963837036089641557922879619729110637997382539771136207851950577937595494145131719149108377813298865350573685187959924685685213024128564020559095558861443465880088146855127027731160733151643292706429845308041466687932912143394757853557159121800644023339675039896474912747094066712836569317683947559334976714054445733535012597716455658405700294711550803044331639683394854264941288619059986522633862886154622975582404301526564131035838365552777983719, 29214929619818811912983377296772756999906238053892245054271578434570872990833805015277605010807494085526771979098010986100867102722354504364459460987290083264092954737625779724099301577900601750939794622980013032447522613756060399427143355169271807171132952049851789598004722074265854068778057922522880069157385485436318543102122357157787642597019028266340067801562185878052429599296600751404659743260494150114728057601265619847290036794857159922042929805207953075826061728968741725552021006256550988912044493141054639034516788865045931761491452989805546879824818126971537686071826068209533188609985774718048970186717, 14899955930336792793532336874433652550803632486127284756045045139078976162820004135413064031687757061259428266818815438988303152287016890920556678040631793791358209442422808682855685434681111953976755186057077138978075649584961165710529290704302479877022210556047020666045632765887758942140333385547072615727311927227434273582149528164393264761783346175792299832792483293739955169992543073799307173757142831644772207319222873715947758419323711550167333785753755257436309486733493101397594020613689699756994964079166434058894869668753968021757636423919978736238191879727598084591393206458790239373388646079939721102019, 14673398278955068686155479632915216548459306863893820609661120423299233897170506303030824041474705437042932194390763164582786686392676339255556697140753062082527733336378259069050782923801616764207883662739430121215853375658099548500234803008019544275549349595024046471564034453251565124431677161800781835802295978619179726427677323387201624247932133436809920109973622786584887439911980329270012182997775746135596745462700945380599436788233994419396805116820624841279039403640023709321625333629279026336137149535840735096743962646896130236540099927993351782437225003946704903027101166904896821594318788767813908143621, 20280046067161228494511964693011607925189128225576621214714747285111401861856895283716929778129710187532589497757106634633558158011441624068423621287362133001790242685850768662352959316956053902511733547702473559869417265278289600214032497013789412184680734228766479031417696074386198787101658312902051430533644025030061685945860477526563742258592813856328076559769513210507767412477832168663332489139160351571899661110099199386226558053922218285975207927539712940995356166941200024723185752399962038024530987301986277361667665594571193574198160441916377914775840146483809060260897201295523903595518769727031805198799]
c= [11956740898676000681217923391083244959343802398551693647808051683201098085925786860259325923496657202490610734593066188119192541953654360791149838109430759578647152111084674213848985805666337165564314651663713048573839234629512412279065078028133462828198749567435497352725684823548698640693058189606015047121716632177220095587192525271580806397172189521815199464499599795072534876883872264208452884680326524888602242579604345084379654555543843635716910332231200784714094206387233055489336506241467093879140961134519199902293557532432549724590885164352161933373347230450303481152191348082596867080525460723859619846511, 7617924002556565535986377328333674602038352364180454509557372930434386538841349121392408315217579430826537255904839088292668060509952422868655885374283232191446407709370726960042119530509614605123700763091299632838426444030888588004056626922663600302427483517770299459926625546685464981793670587522402308415766923937226916278033403817780774034683308959643099199449391744089291991427217727194483987088412098125295023823065517365360795002823279536815650932749767076865670166271996294871030977107872592857161322913217260696594367217266411317705042858328305316566166616652852980036593739637044803512310496203436813764047, 13912186408628192093102456995240476610411258652802502095280231966102426927608780700027690589430564850835548322650470162753110865933021472506414983583982943230804133935740936614364177538589392112444879316271830729156055320464727367081907779336681030873682964025533234466980996263156887858124367314506468113019905624286198795096953156749733889713285238944046791297991384098831981774955246770733249129156544643605845729652564921576168690992180495411141798471595576178877234004527277756940419123193046288667491703745072195652449431405002407369710986663177915556299662117282141526405045072898840345061988077717478644699195, 28151047821311790586654008646272026570203746847773242899470299841804378472238171169845658004505448737609251915534082288116058137597306984329603380499483837627838932208830739270863217879546458738981166190609407521750270436715929383781225826703092626586095662676231555860878020521497103382257310363352483224928869712651319469816486081593510165222703939770302104975304690120438316679590467121354125639984662877942600341754120216543238715216170576755028887801562314292693871177035424282450968601507796439594919815085853977287392661607535263555445304889560066548118005709193876675846635477882748658848449766684619409997764, 1641866907675812307158147466098525995568933100887920593661179894014826559030682611392712739180141245398627410191380835109558529910095201005200711964724993475349558777540480811714913001221241980441581902822651571637788004419619484325091653571031451634171303873510756444029339180522599604509103240976358247449436526548062538482194943835627632213233420980448883740505798304364718417158999202414413637581281515412433217191451969853690769700541636698201366045862585995973367729615578705936831780051243505714470959150903516229079262340719254590526950200736567380148666895554252762360880846371421036055911232247902178027098, 382350300809625490229427917644431600331855926541015620919041152776462790446391934704031993509057171708190329936892116142545448064375721955400171442465376939732228344933537532677737828576613368914949346356456974893777500690335635619420851458465053628042402549131638492877696454132406754021316447157373223249569749603336423287352791974874983914815357821300226228015465299158724411567423576601972789591633588882079724777254196223044373267094950240018214443519835836415254891625590880239474687988109749579857581426177504162298866555973467591069030112993584190647627433798676664265981630222020576719540689393708642272345, 18650843962384693164739866449054167511266301548794763731088968531269372938131549617037207479422171489508187720596594411488759655047901286999042039069684053836516964325563913930222262031071015823369271773647345468921678027147470820413466788362348635636057631047856875878068214712699868435460966917704137550074315247963286783044862698124813553966031040673920145877940284880863430545790971292403623356675844675879375405728961325757767236717374878397410206354351379127290881775061798760018525283265941815866955474404362045296315737502666487745657969341519692398106009614083877837357478990682262691984420107763648449778265]

原理

中国剩余定理及部分裴蜀定理证明

中国剩余定理课程

原理证明

实际应用

代码

import binascii,gmpy2
from functools import reduce

import libnum


def CRT(mi, ai):
    assert(reduce(gmpy2.gcd,mi)==1)
    assert (isinstance(mi, list) and isinstance(ai, list))
    M = reduce(lambda x, y: x * y, mi)
    ai_ti_Mi = [a * (M // m) * gmpy2.invert(M // m, m) for (m, a) in zip(mi, ai)]
    return reduce(lambda x, y: x + y, ai_ti_Mi) % M

e= 23
n= [13700568188515160652483333122748856122721197793561758976293940196437611129096187147049018844770801852491509905633421086860525538786202094426963328030251710764571262136174896745533638173611350459716214924297588461960177050085385463667053134112771796358074472935345700519739991250404101653259068109069693105921388873407341327391535695855870048544246046807524271999074571290297887397122751189238913097314211648891658786959026354758174645247220351373112768023740548658853638361571194694899655444114676642455442372865402013423716810043521278757792135057542028337381224680456644807085272591758332208055210218120184762933993, 12455303951778295101801876746865726762837380068225611327265475119171234220566439286424157465915935073825839673377690927685328334906307316474567186387631653801487281448621083840044622749158794717243547992072439308091388396577613505544620596436291129920864908674330398567591089739953054198863265589615640925745448938637009162522951734388734884333210018733280942210441939903191498896601489219385238879930891399742641138070096026008226581854996694584005317481033177457738077410685570860098544905752983525186623046625831970650060102227916725290755005373441583687173317035035580381484364030548806838563780182184117638395501, 11312913453345524997229175092303757066349809787030135927591246090443816441487008566337534259925791562593802909853876625626317525202428762422138834267165059103366474521447755350822619474026723784588743249816343322663039545930277057837056152601616900790058365628051926865192020616084647924562898079954569875871488048485269581903324695594743584490301132714735102846843035514174635115834382345956826120332925240425711055383445735314612014526078453624636064136731525847521062469732411461240879728208804879621960486763810048962817360272134393185930002946977732438576414921250013379633385546522773969341316069572502067565747, 19273688926871530751707885170718573691217157450567879434223457628340410073625895093788197974441685806302563195850728310991029886375715086122432340760177266985524985445504300034480827487797904941865418089597333968798898696588493471468263648636085443020434703464184815215924633364352735339920297191301112596913193981943417483120540953061378442416926357165828400001655707467493126093621482473840789855669296212432210460828627914111587469312179918093681028472281824867507358588256781382024745011058883359327063772375423890907634909474243733397473408057822868275644578237140525612613960087777442779675214209932962161127943, 25824403380218842654152117237181863815407686057920357548100132783016208234216157331481187013858706620084532009147859360032194662194329147430352381352060599665383607132414222783152103706812942495504805443853663820643284400132519740763181995336671760074736189118849190911417412125673622718186682930944463719251663826122062414169185281402187745799450127860616811214434583738617470847946117017912241156196170781549212311773302997289690360334428053433645188479934679156573770259457673448241437007751122166255146634172359683608410225806629185780976706769275891277564054509652711969428966369382807140328871035548244913540169, 27237916069051621208940446912652352983034283876768722877796629630339066194659652050347720419800886409125794947519574028544026594230991606608793723513349031053967598250588096756917851047427400805606694825815650771281434785207392911507124225263256982256339868047939184615897450178154018301408865653899046967323372600912627209194957697714349971037547547785817038582309482843956504640495722872808769284795831606211370129997371039857944461416328980185572754574947986464294124047090215456723501364524474569642506285260702179251484768225200095243277847312804129809104143492271538375785121251371642879445405237226218130294767, 13761550682262178277138207445908812895938004012620351458812077456012342912081457948142730381037941264721223863482179216010551793547021574285408780459622610402725800322968427850107196669966179328339837806343597136218927944640487794959105652921590477743490006234776475206318254765423468761009179359533340573903819987444132938579714590504929528901380380034611797641640102025769022580055379262631658712636898183456153010636153333354330556615811465638688432337372481631547224635135648075131524783033767896216049834072882777559679890752875405582498757130694817571975439400501682753249614034942783158191876673449277964305873]
c= [10262571808823462518706222972617543597862568988621892788603169566061143066015712397590162941689759961146172690260488971865965270847230222579998032904557938430984766267711048364907947168116473908091952262274847901197798670702630932509348193160049011343984674456154980133706472252009228877741952811774717803218313244040775956381945077497379634101671865923305021804060521682939202170177994307021066512676052755208342422597702905467231418454913781792876325613132181844091995047630699929420681514255787561417787538399764114936771546416271603555435195286433694761222982635917086486380929164535357220194188751490847126159740, 1873760069623225193188031460164577168629510321843511590851589581010158323091884037245625334264450576423497513703748949943402486554235195486945608003604913492410550727032646952732075387833483434157962823847945961417788077590746865603009614636801926695485643494439910816287002493987681839263137321312158281577409606512588038571503481880205375876372759847610515728629030784895468324627007475548811579324164095761843942789779697129082973879068202809855392853491223029896314818656151121278599338954208895547796950391203204627158727359612310869523861493123901912234283765154942764948742461112728821107134608346552771856775, 2985895977894993412250356564280621188757701877004747248029655606908178453788442472530624315824217412687521627124641549636268771426175593603860596969406918746968428475480360839574070154578348252212233965555420185919910549233104881737429986120779245582625147836249604511991694099504498456423355415033891952572068957140136031237587821914297743550751703500164233251775829591163214908665505948671743637428615178406048668071123208829673815143306105215918457316827849469724561259085924020618664008688924504157202910867055508798021785392339533763892777711399815389010578953671416118696256122691527492893238690603105740871718, 880226958648330570665826652923585021064905285913220564535802601268914731939998238851663053132946194395728683681709691206818341165883097568804208974913295560837751365921375933221025439628586836402981502674560586284377581275819082460923772292780487491196858992362166740159608419089452540222602172839570711702715638458570267373629408280794214751990345330692342439212475521544906222647038911039746667297765160642325197077286500302972512842670715220866427191331087678451078964988930072707946282911276517877581001397844626280393814317485128907214187598723285030652543787338988559227984102314239323999288888886062656553567, 2009815427590067013904234705045801411676517862085803426907991060580056876965631979890272588810800230952582542504850877216565503823555945840629024122371840947339558621619080946766065959900677138148030357494710396126783369878070540451138925897438184723977799391715647904517833046633527545658064968373331747651285453005992951298693244135497529999014011663505125408546171884008627711191184419674138689402575260876247393334319284308455639799976027283117878360299913911527890869762030625362974305707352360014964055595635315501016094747111266795155708691399809263809612237731990725856751947329733607523318847566974421507377, 5694700766209667533320463555578774304413921444532095100497641465531621818677278187178007777107102216001903166590706266461389108866563137126658591265596096815630888192401258893389043674230339983362206002697721033273220169349689433933228398864735569502059227668658884754437859192804614688078126017106973898338983058467903273433629800893427045854677794419302456422469488313296020469202479512874455184512957276727018667852597050339727765639174070344434646695283305954814336208535975320481890216924783115781802398152316171967550392347431746885369490458690822632544727994467024208594657404613355215378203965583472028051158, 10292024155412613173825075050556970628998306804602106049394871162726180325842644363271001627039660982320232377250177866906798633433125147372046294230795160430975886694419367570376173140902999001496377201160021928316891425794054040646925354276987039659647583093660753953920769021487949471906220620446860851971969844544591399518592683848757784465531598787547279741438244737906014906621222662915117890417807671575763023265920422409800110274912550502682376498609611973173660997965660328963204286476887664127188442751055758474381180365051193094521479396706496869721757475497142256079170254820437945136475911435012491537989]

m=gmpy2.iroot(CRT(n, c), e)[0]
print(m)
print(libnum.n2s(int(m)))

2022.1.1

BMZCTF

“明天要考了，我现在突击一下”

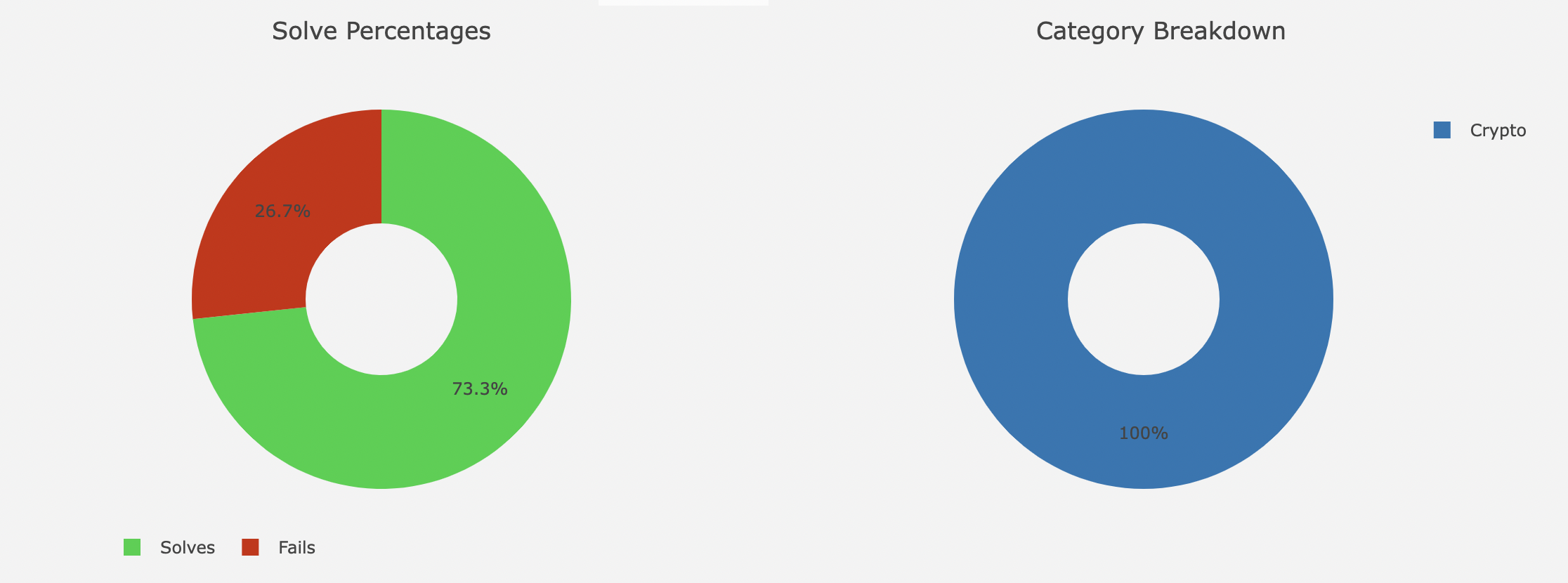
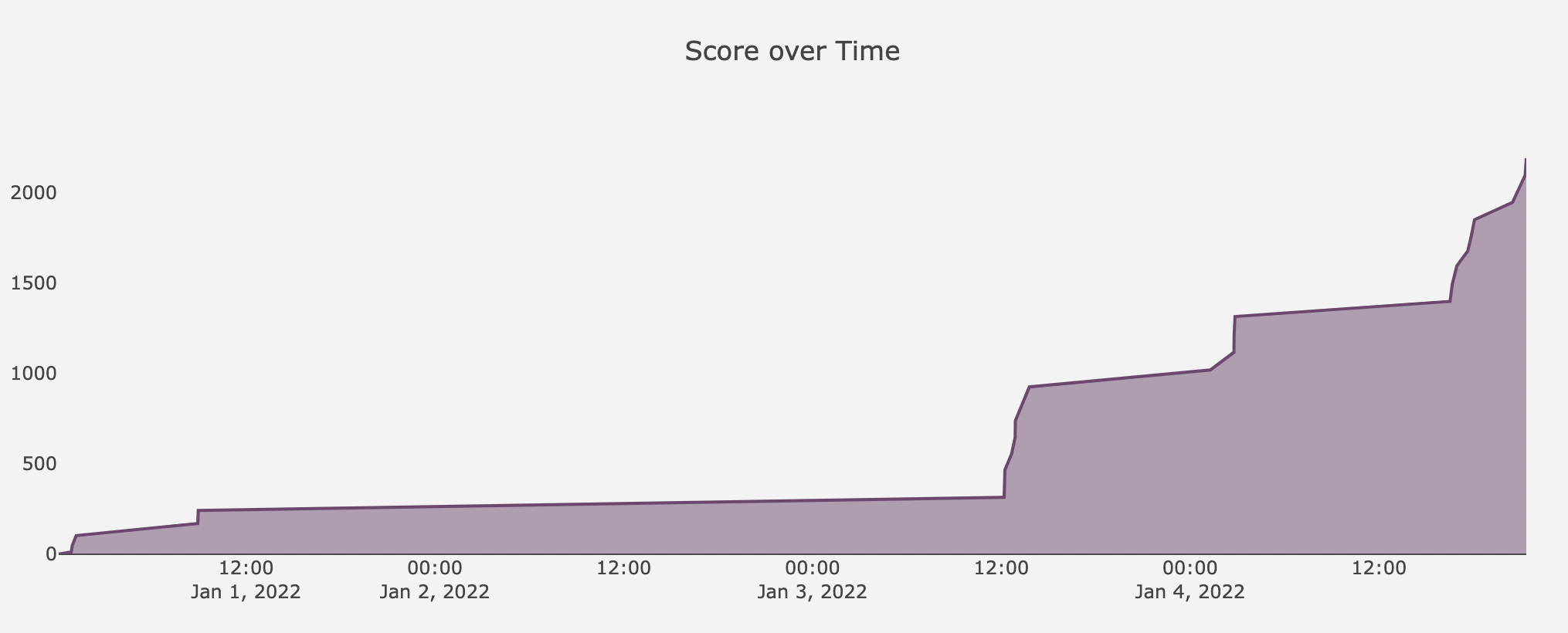
为了明天的正式赛事，凌晨做了下BMZCTF平台的练习题。
采取动态分数，题目后面的即是做时的分数。

新年快乐！

4进制·1

题目

1212 1230 1201 1213 1323 1012 1233 1311 1302 1202 1201 1303 1211 301 302 303 1331

py3代码

a = '1212 1230 1201 1213 1323 1012 1233 1311 1302 1202 1201 1303 1211 301 302 303 1331'
a = a.split(' ')
for each in a:
    print(chr(int(each, 4)), end='')

2018 AFCTF Morse·1

题目

-…./.—-/-…./-…./-…./…–/–…/….-/-…./-…./–…/-…/…–/.—-/–…/…–/..—/–…/–…/….-/…../..-./–…/…–/…–/—–/…../..-./…–/…–/…–/….-/…–/…../–…/—-./–…/-..

题解

网站解码

2018 HEBTUCTF 社会主义接班人·1

题目

身为社会主义接班人的你，核心价值观你会背吗？

自由爱国自由平等自由文明平等自由平等平等自由和谐平等自由自由公正法治诚信民主公正平等公正友善自由法治公正公正友善敬业法治公正公正自由公正民主法治和谐公正公正公正诚信富强公正公正法治公正公正友善法治法治文明公正公正公正友善法治法治和谐公正自由公正平等公正诚信和谐法治爱国公正友善自由法治诚信和谐

题解

社会主义价值观在线解码

栅栏密码·1

题目

fa{660cb679d7866ffalg7d27e041cfbd18ed}

题解

def enFence(string, space): # 解密
   s = ""
   global whu
   for i in range(0, space):
       for j in range(i, len(string), space):
           # 不能越界
           if j < len(string):
               s += string[j]
   print(s)
   whu.append(s)


def deFence(string, space): # 加密
   s = ""
   if len(string) % space == 0:
       key = len(string) // space
   else:
       key = len(string) // space + 1
   # 小于间隔继续
   for i in range(0, key):
       for j in range(i, len(string), key):
           # 不能越界
           if j < len(string):
               s += string[j]
   print(s)


from math import sqrt

def factoring(n):
    '''对大数进行因数分解'''
    if not isinstance(n, int):
        print ('You must give me an integer')
        return
    #开始分解，把所有因数都添加到result列表中
    result = []
    for p in primes:
        while n!=1:
            if n%p == 0:
                n = n/p
                result.append(p)
            else:
                break
        else:
            result = map(str, result)
            result = '*'.join(result)
            return result
    #考虑参数本身就是素数的情况
    if not result:
        return n


maxData = 10000
#小于maxData的所有素数
primes = [ p for p in range(2, maxData) if 0 not in
        [ p% d for d in range(2, int(sqrt(p))+1)] ]

whu = []
m = input("请输入传统栅栏密文：")

len_m = len(m)
print(len_m, '=', factoring(len_m))
try:
    for each in range(1, len_m):
        print('每组字母数：', each)
        enFence(m, int(each))
except:
    print('错误!', '输入密文位数为', len_m)

for each in whu:
    if "flag" in each:
        print('\n我觉得flag是这个！你看呢？\n{0}'.format( each))
"""
我觉得flag是这个！你看呢？
flag{76d6207ceb064719cdf7b8d6168fefda}
 """

Ook·1

题解

Ook码在线解码

题目

题解

祭出网络厨子CyberChef

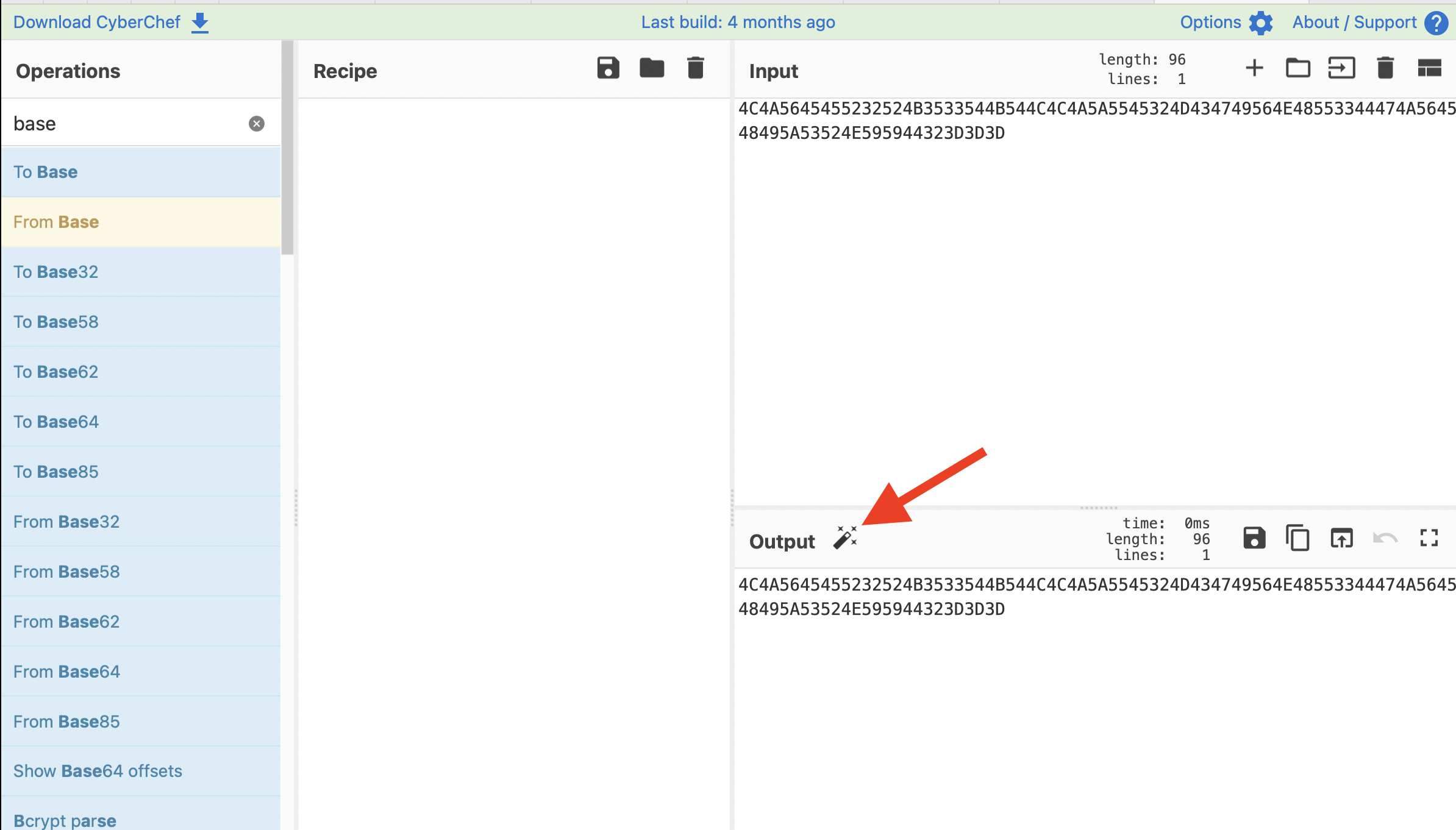
接下来，无脑点击结果优化！

结果放进栅栏, 解得:

我觉得flag是这个！你看呢？
flag{0939_F2A_BACD0}

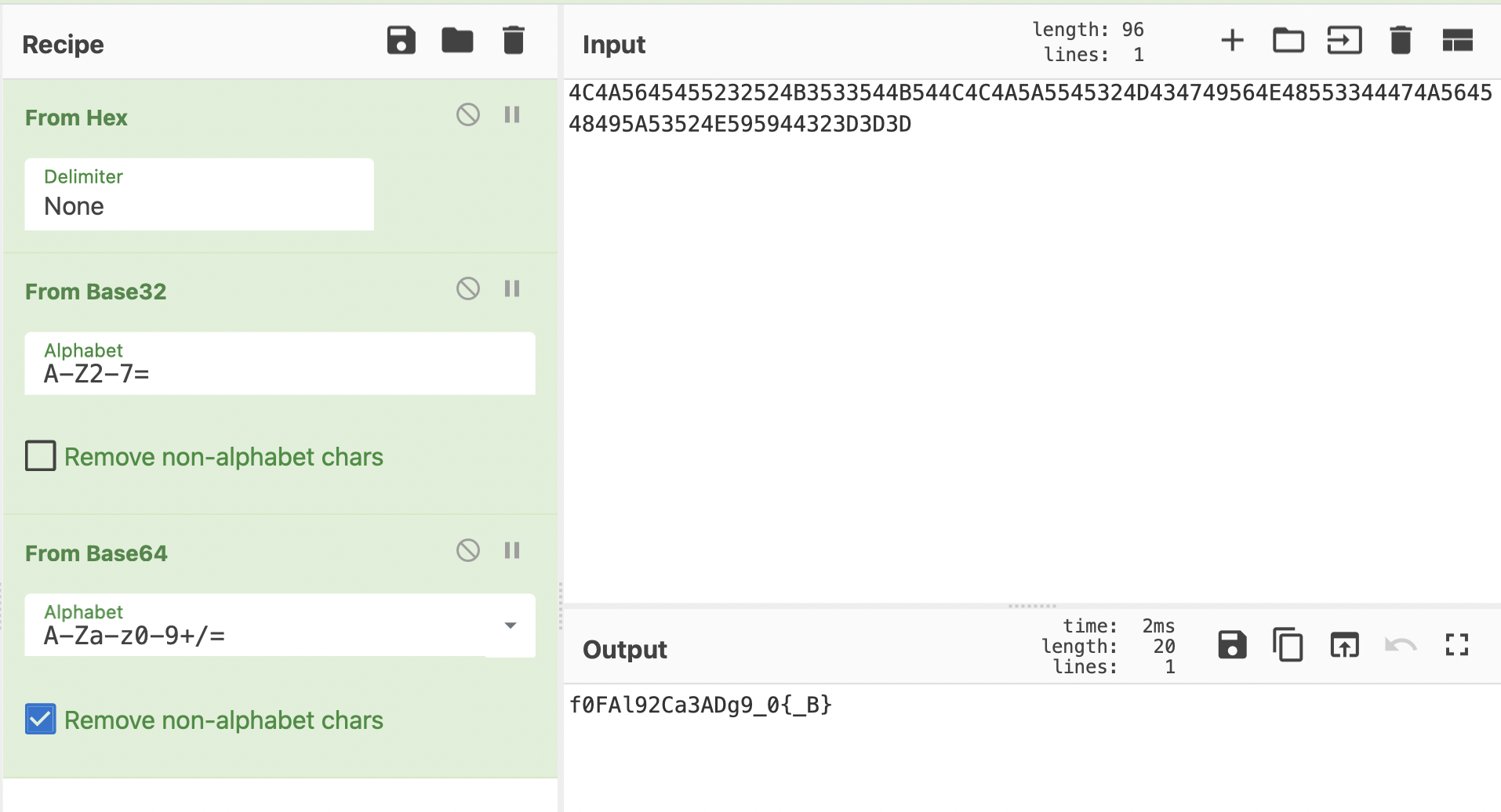
easy_base·13

题目

“影分身之术*40”
下载后，打开看到巨多的base64
懒得写代码，厨师👨‍🍳烹饪40次

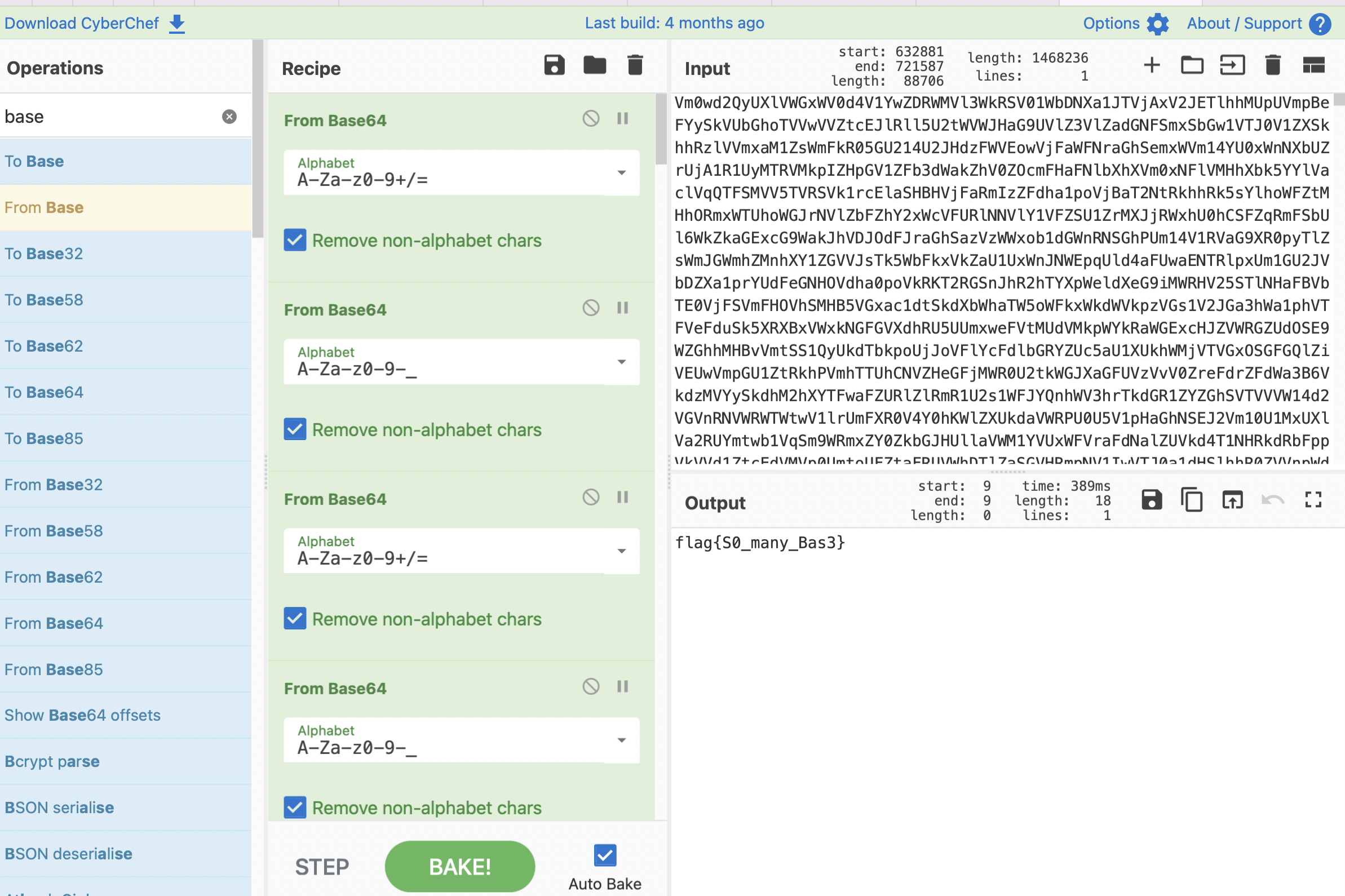
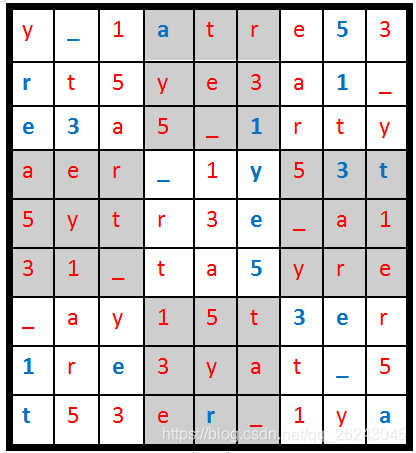
2018 HEBTUCTF Sudoku&Viginere·39

题目

下载附件，为一个doc文件，打开后发现是一个数独游戏，和一个密码。

题解

完成数独后：

维吉尼亚解码,得到：

HEBTUCTF{15_1t_3a5y}

看键盘·56

题目

ujn njkm ijnmhjk fgtrdcv tgvgy njkm hjuygbn ijnmhjk

提交：ctf{}

题解

常规又离谱。

根据古典密码大全(2),没找到

于是便仔细看键盘，发现每组连在一起，轨迹像字母

第一次尝试

i/j/l n ? e y/v n e ?

第二次尝试

jnteynet

第三次尝试

lnteynet
l为L小写

第四次尝试

我一眼就看出是你！互联网
ctf{internet}

错了！

第五次尝试

ctf{Internet}

意料之外，情理之中

成了！

2018 AFCTF 可怜的RSA · 69

题目

flag.pem 和 public key.pem

题解

• 改公钥后缀，放入网站解析（其实python本身就可以做到

• 得到n,e 进而得到q、p、phi、d

• flag改后缀能打开，看到base形式的东西，直接base解码没东西

  GVd1d3viIXFfcHapEYuo5fAvIiUS83adrtMW/MgPwxVBSl46joFCQ1plcnlDGfL19K/3PvChV6n5QGohzfVyz2Z5GdTlaknxvHDUGf5HCukokyPwK/1EYU7NzrhGE7J5jPdi0Aj7xi/Odxy0hGMgpaBLd/nL3N8O6i9pc4Gg3O8soOlciBG/6/xdfN3SzSStMYIN8nfZZMSq3xDDvz4YB7TcTBh4ik4wYhuC77gmT+HWOv5gLTNQ3EkZs5N3EAopy11zHNYU80yv1jtFGcluNPyXYttU5qU33jcp0Wuznac+t+AZHeSQy5vk8DyWorSGMiS+J4KNqSVlDs12EqXEqqJ0uA==

Punchline

风二西的课程讲了，这里才看到实际的应用。

text = 'GVd1d3viIXFfcHapEYuo5fAvIiUS83adrtMW/MgPwxVBSl46joFCQ1plcnlDGfL19K/3PvChV6n5QGohzfVyz2Z5GdTlaknxvHDUGf5HCukokyPwK/1EYU7NzrhGE7J5jPdi0Aj7xi/Odxy0hGMgpaBLd/nL3N8O6i9pc4Gg3O8soOlciBG/6/xdfN3SzSStMYIN8nfZZMSq3xDDvz4YB7TcTBh4ik4wYhuC77gmT+HWOv5gLTNQ3EkZs5N3EAopy11zHNYU80yv1jtFGcluNPyXYttU5qU33jcp0Wuznac+t+AZHeSQy5vk8DyWorSGMiS+J4KNqSVlDs12EqXEqqJ0uA=='
c_bytes =base64.b64decode(text)
rsa_components=(n,e,int(d),p,q)
arsa=RSA.construct(rsa_components)
rsakey = RSA.importKey(arsa.exportKey())
rsakey = PKCS1_OAEP.new(rsakey)
decrypted = rsakey.decrypt(c_bytes)
print(decrypted)

代码

# flag 文件 改txt后base码
from Crypto.PublicKey import RSA
 
import gmpy2
 
import base64
 
from Crypto.Util.number import *
 
from Crypto.Cipher import PKCS1_OAEP
 
 
 

e = 65537
p = 3133337
q = 25478326064937419292200172136399497719081842914528228316455906211693118321971399936004729134841162974144246271486439695786036588117424611881955950996219646807378822278285638261582099108339438949573034101215141156156408742843820048066830863814362379885720395082318462850002901605689761876319151147352730090957556940842144299887394678743607766937828094478336401159449035878306853716216548374273462386508307367713112073004011383418967894930554067582453248981022011922883374442736848045920676341361871231787163441467533076890081721882179369168787287724769642665399992556052144845878600126283968890273067575342061776244939
b = (p-1) * (q-1)
n = p*q
d = gmpy2.invert(e, b)

text = 'GVd1d3viIXFfcHapEYuo5fAvIiUS83adrtMW/MgPwxVBSl46joFCQ1plcnlDGfL19K/3PvChV6n5QGohzfVyz2Z5GdTlaknxvHDUGf5HCukokyPwK/1EYU7NzrhGE7J5jPdi0Aj7xi/Odxy0hGMgpaBLd/nL3N8O6i9pc4Gg3O8soOlciBG/6/xdfN3SzSStMYIN8nfZZMSq3xDDvz4YB7TcTBh4ik4wYhuC77gmT+HWOv5gLTNQ3EkZs5N3EAopy11zHNYU80yv1jtFGcluNPyXYttU5qU33jcp0Wuznac+t+AZHeSQy5vk8DyWorSGMiS+J4KNqSVlDs12EqXEqqJ0uA=='
c_bytes =base64.b64decode(text)
rsa_components=(n,e,int(d),p,q)
arsa=RSA.construct(rsa_components)
rsakey = RSA.importKey(arsa.exportKey())
rsakey = PKCS1_OAEP.new(rsakey)
decrypted = rsakey.decrypt(c_bytes)
print(decrypted)

small_rsa·72

题目

# -*- coding: utf-8 -*-
from Crypto.PublicKey import RSA
import libnum
import uuid

flag = "flag{***************}"
rsa = RSA.generate(4096,e=3)
p = rsa.p
d = rsa.d
e = rsa.e
N = rsa.n
m = libnum.s2n(flag)
c = pow(m, e, N)
print "[+]c:",c
print "[+]N:",N
'''
[+]c: 3442467842482561323703237574537907554035337622762971103210557480050349359873041624336261782731509068910003360547049942482415036862904844600484976674423604861710166033558576921438068555951948966099658902606725292551952345193132973996288566246138708754810511646811362017769063041425115712305629748341207792305694590742066971202523405301561233341991037374101265623265332070787449332991792097090044761973705909217137119649091313457206589803479797894924402017273543719924849592070328396276760381501612934039653
[+]N: 691316677109436623113422493782665795857921917893759942123087462879884062720557906429183155859597756890896192044003240821906332575292476160072039505771794531255542244123516929671277306361467074545720823735806308003091983427678300287709469582282466572230066580195227278214776280213722215953097747453437289734469454712426107967188109548966907237877840316009828476200388327329144783877033491238709954473809991152727333616022406517443130542713167206421787038596312975153165848625721911080561242646092299016802662913017071685740548699163836007474224715426587609549372289181977830092677128368806113131459831182390520942892670696447128631485606579943885812260640805756035377584155135770155915782120025116486061540105139339655722904721294629149025033066823599823964444620779259106176913478839370100891213072100063101232635183636552360952762838656307300621195248059253614745118852163569388418086291748805100175008658387803878200034840215506516715640621165661642177371863874586069524022258642915100615596032443145034847031564356671559179212705466145609698475546210994748949121359853094247990533075004393534565421776468785821261291309463205314057882016266066365636018084499158806717036972590848458891019171583268920180691221168453612029698510271
'''

题解

我一眼就看出来，你的e才等于3.
了解到低加密指数攻击

代码

import gmpy2
import libnum
"""
a,b = gmpy2.iroot(mm, e)
a 为 mm开e次方的结果，b为是否刚好开得出来（True/False）
"""

def de(c, e, n):
    k = 0
    while True:
        mm = c + n*k
        result, flag = gmpy2.iroot(mm, e)
        if True == flag:
            return result
        k += 1
n= 691316677109436623113422493782665795857921917893759942123087462879884062720557906429183155859597756890896192044003240821906332575292476160072039505771794531255542244123516929671277306361467074545720823735806308003091983427678300287709469582282466572230066580195227278214776280213722215953097747453437289734469454712426107967188109548966907237877840316009828476200388327329144783877033491238709954473809991152727333616022406517443130542713167206421787038596312975153165848625721911080561242646092299016802662913017071685740548699163836007474224715426587609549372289181977830092677128368806113131459831182390520942892670696447128631485606579943885812260640805756035377584155135770155915782120025116486061540105139339655722904721294629149025033066823599823964444620779259106176913478839370100891213072100063101232635183636552360952762838656307300621195248059253614745118852163569388418086291748805100175008658387803878200034840215506516715640621165661642177371863874586069524022258642915100615596032443145034847031564356671559179212705466145609698475546210994748949121359853094247990533075004393534565421776468785821261291309463205314057882016266066365636018084499158806717036972590848458891019171583268920180691221168453612029698510271
e= 3
c= 3442467842482561323703237574537907554035337622762971103210557480050349359873041624336261782731509068910003360547049942482415036862904844600484976674423604861710166033558576921438068555951948966099658902606725292551952345193132973996288566246138708754810511646811362017769063041425115712305629748341207792305694590742066971202523405301561233341991037374101265623265332070787449332991792097090044761973705909217137119649091313457206589803479797894924402017273543719924849592070328396276760381501612934039653

m=de(c,e,n)
print(m)
print(libnum.n2s(int(m)).decode())

以上为凌晨时分的题解。

今天主要在打BMZCTF赛事，虽然没出什么成绩但收获不小。

1.2

中国剩余定理及部分裴蜀定理证明

中国剩余定理课程

原理证明

实际应用

1.3/1.4

RSA·N不素

特征是，生成多个N的时候，用了同一个素数p/q

对策

求两个的N之间的公约数p。

代码

import libnum
import gmpy2


e= 65537
n1= 18851781425565649500243914718895527060598553785142033499277947796047289729069551538151421839511239897691881228121437622923274745439286192958624933347473814433650645821240330239352230328910532686189064529002598986350545013596873280380093139589440286483854335646063005690269032198568724965964443111093291700142910652223408636268615176273268372177721667944316123253596652992256076572634227395015036348109972259736684061785035583511127926569341967394058493301139935304361924639075754092181040235419401702148068770694697982444290753353433701503833775179671108406498799549700127209151389161427718168658930877516526900193773
n2= 24141384186719901100738328229558939321137195844627407412035205930880546126459260897433418685279927024995699136588216700770429628894224051287181657357533218989737870319139269421990248988961435374202640406264110282763206906390508271179764960952342404379846442988489435158217691170804372863828966379599925114485971708200189788312061335938149982724447336254731731196164294152411281627551943972751739099703406466680639123738668207648503911709799873188331259979032169198913999856215096219340617703116234922400948884716827963616800355410477122406692338452507358998811789750057925245184372948089354754021196407808558611706347
c1= 11233930138929485738604185458820792679941706517184575056860307907280050814616639358486313129298273947905894904145194035804995663173314907762677924041275132974029028894644172713486633713023630611556983846927634063704894533048653309657581762974450289360550659261899944333557732087882069544235529266455787027619668939220511057340231613645208599303911724024926701608537602920797245075262273603379467945283128416767718651714209330369788240996832207630345743245279821753430782200336283582459635492184924556145031704499178500242816865275291936063430100028447772122941596704727728675661250380470986371668037469383671505328135
c2= 5585224206647236865248808202221713289466135149339680308821203835812670001259895780508640505222648200259525489427033258746992319005320440650548405653844536422632581252608192223771882550003217335273112474383014796651892287737753603533030776710121680439078567046997872719450037145665867123925472406058893384600128119493338790196284996386511009366274826447064392594100457497289556291407982935292829015102796178711091471748295065093460144885719356062242014650190112796869173536886083200906303200902844575328314123662659807283984619970501020349836850699532193026247740142876327310689901499496665093919484517214474842110431


#求最大公约数
q=gmpy2.gcd(n1,n2)
p1=n1//q

phi_n=(q-1)*(p1-1)
#求逆元d
d1=libnum.invmod(e,phi_n)
m=pow(c1,d1,n1)
print(m)
#数字转字节，转字符串
print(libnum.n2s(int(m)).decode())

RSA·dp泄漏

什么是dp

$$ dp = d mod (p-1) $$

攻击原理

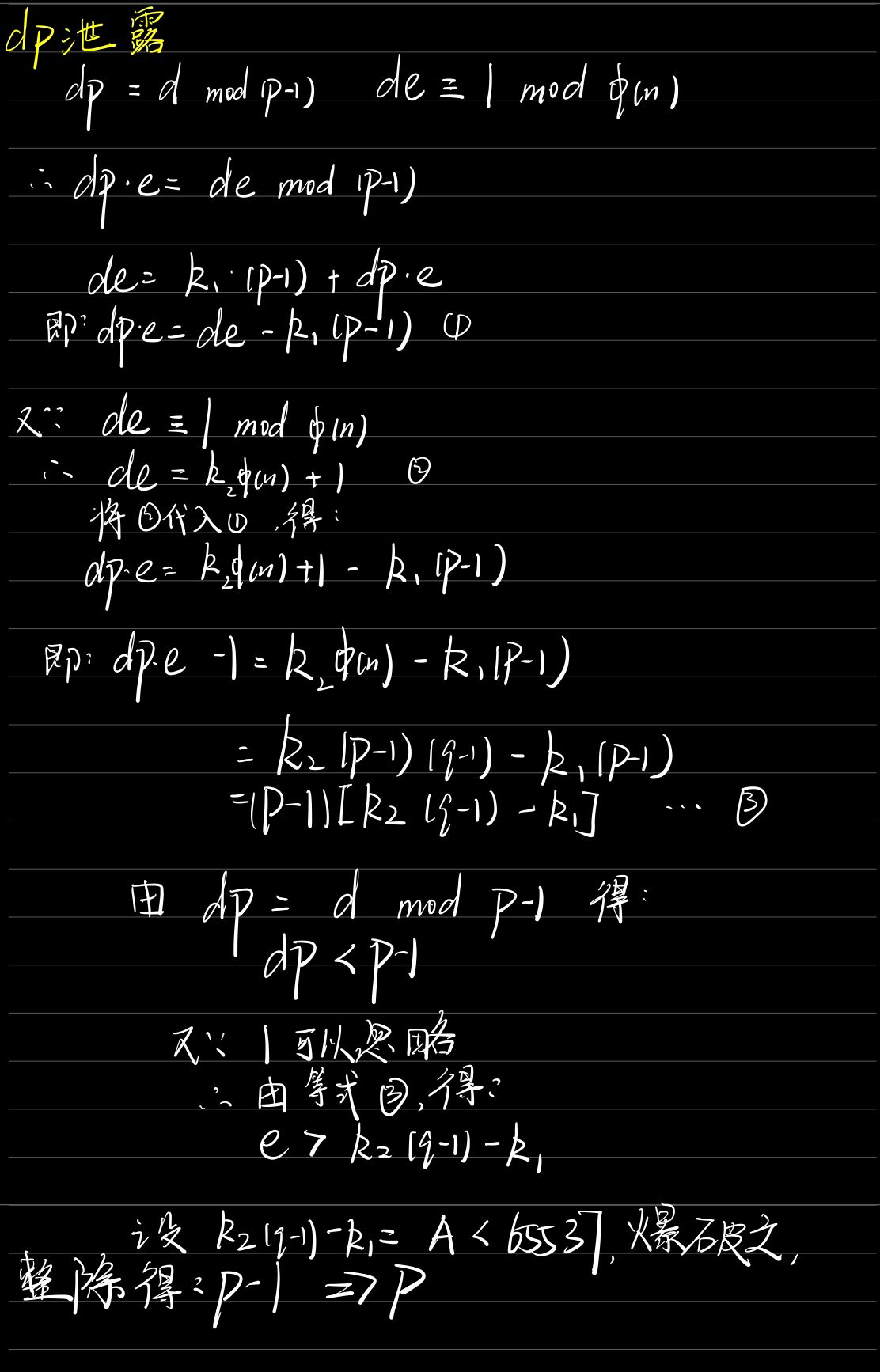
代码实现

import gmpy2 as gp
from Crypto.Util.number import *

e = 65537
n = 156808343598578774957375696815188980682166740609302831099696492068246337198792510898818496239166339015207305102101431634283168544492984586566799996471150252382144148257236707247267506165670877506370253127695314163987084076462560095456635833650720606337852199362362120808707925913897956527780930423574343287847
c = 108542078809057774666748066235473292495343753790443966020636060807418393737258696352569345621488958094856305865603100885838672591764072157183336139243588435583104423268921439473113244493821692560960443688048994557463526099985303667243623711454841573922233051289561865599722004107134302070301237345400354257869
dp = 734763139918837027274765680404546851353356952885439663987181004382601658386317353877499122276686150509151221546249750373865024485652349719427182780275825


for a in range(1, e+1):
    if (dp*e-1) % a == 0:
        if n % ((dp*e-1) // a + 1) == 0:  # ! 关键，易漏.要求n被p整除
            p = (dp*e-1) // a + 1
            q = n // p
            phi = (p - 1) * (q - 1)
            d = gp.invert(e, phi)
            m = pow(c, d, n)
            print(long_to_bytes(m))
            break
    else:
        a += 1

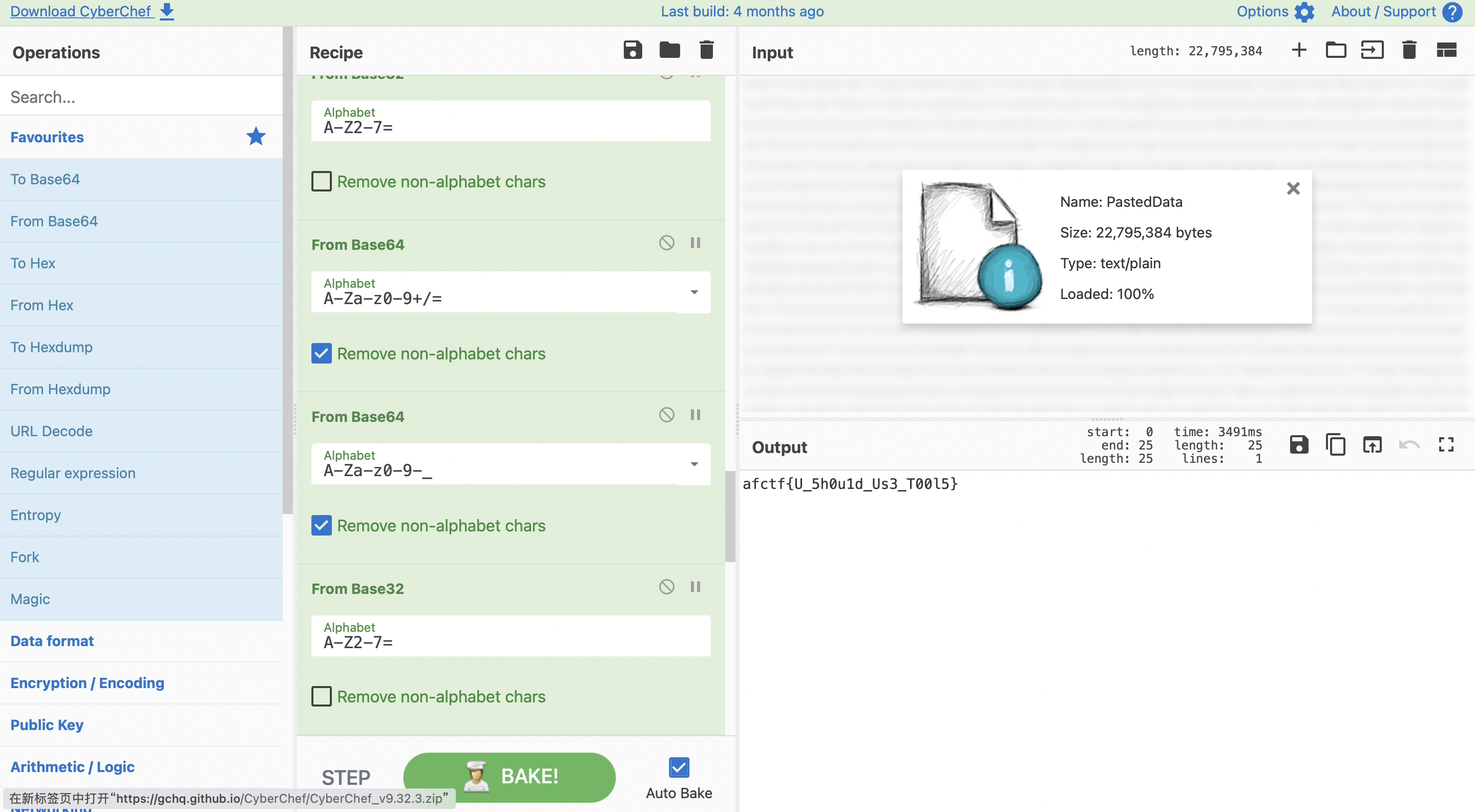
2018 AFCTF BASE · 100

题目

打开后真的好长的HEX，杂了base64、base32

题解

厨子👨‍🍳一把梭，啥都不说了，开烹！

点了大概十几下数据美化

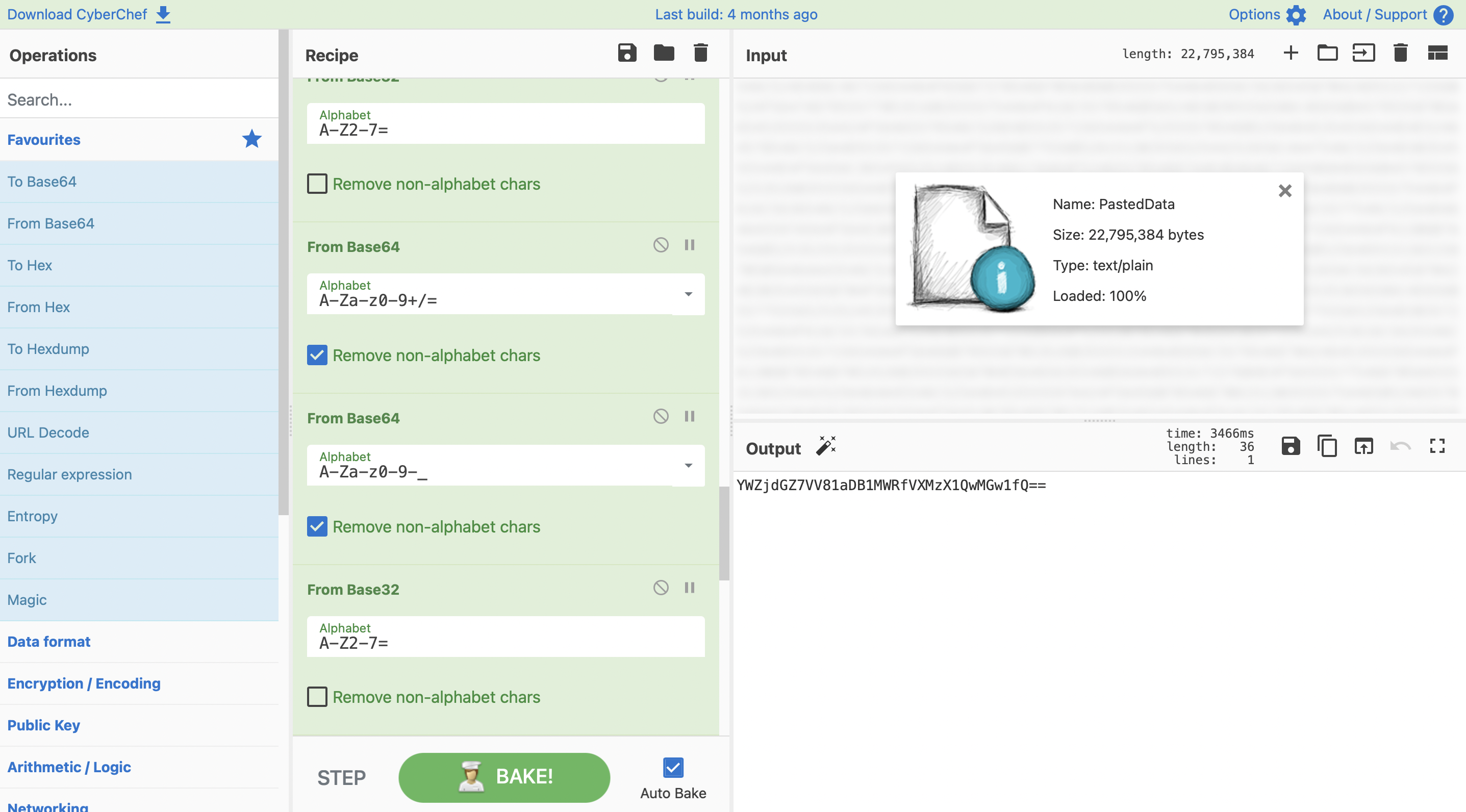
CyberChef，YYDS！（稳定性与可处理的数据量都好完美

看的出来吗 · 82

题目

有一串神奇的字符串bE0veldtTDs7NzlTe3hzbSFYSj5Sa2U6eyQ4NyVrI3FvWFU6Qls7QlVK，还有一张纸条写着589164

看了后，完全没思绪。

长这个样子，又有key的加密方式确实是不知道…

题解

经过base64解码、base91解码、base58解码得到

https://base64.supfree.net/
http://ctf.ssleye.com/base91.html
http://ctf.ssleye.com/base58w.html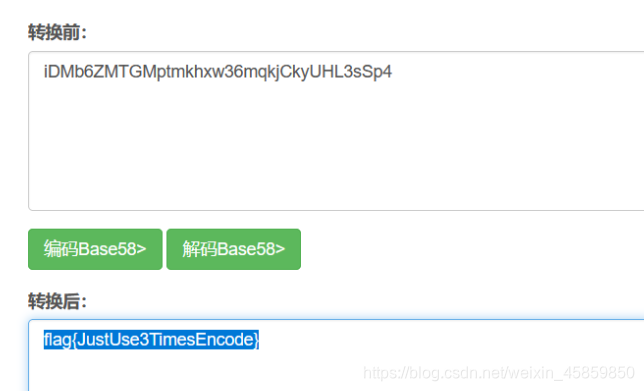

恐怖如斯，原来是base的58、91、64（说来好像遇到过，看来印象不够深刻

键盘之争 · 84

题目

你听说过键盘之争吗？提交你找到的字符串md5值。

ypau_kjg;”g;”ypau+

好的，👀看了半天，啥也没看出来

题解

键盘布局有qwerty、dvorak、colemak
此题考察的是将qwerty布局转为dvorak

代码实现

import hashlib

dic={r"'":"q",
 
r",":"w",
 
r".":"e",
 
"p":"4",
 
"y":"t",
 
"f":"y",
 
"g":"u",
 
"c":"i",
 
"r":"o",
 
"l":"p",
 
r"/":r"[",
 
r"=":r"]",
 
r'"':'Q',
 
r"<":"W",
 
r">":"E",
 
"P":"R",
 
"Y":"T",
 
"F":"Y",
 
"G":"U",
 
"C":"I",
 
"R":"O",
 
"L":"P",
 
r"?":r"{",
 
r"+":r"}",
 
"a":"a",
 
"A":"A",
 
"o":"s",
 
"O":"S",
 
"e":"d",
 
"E":"D",
 
"u":"f",
 
"U":"F",
 
"i":"g",
 
"I":"G",
 
"d":"h",
 
"D":"H",
 
"h":"j",
 
"H":"J",
 
"t":"k",
 
"T":"K",
 
"n":"l",
 
"N":"L",
 
"s":";",
 
"S":":",
 
r"-":r"'",
 
r'_':r'"',
 
r";":"z",
 
r":":"Z",
 
"q":"x",
 
"Q":"X",
 
"j":"c",
 
"J":"C",
 
"k":"v",
 
"K":"V",
 
"x":"b",
 
"X":"B",
 
"b":"n",
 
"B":"N",
 
"m":"m",
 
"M":"M",
 
"w":r",",
 
"W":r"<",
 
"v":r".",
 
"V":r">",
 
"z":r"/",
 
"Z":r"?",
 
r'!':"!",
 
r"@":r"@",
 
r"#":r"#",
 
r"$":r"$",
 
r"%":r"%",
 
r"^":r"^",
 
r"&":r"&",
 
r"*":r"*",
 
r"(":r"(",
 
r")":r")",
 
r"[":r"-",
 
r"]":r"=",
 
r"{":r"_",
 
r"}":r"+"}
 
s=r'ypau_kjg;"g;"ypau+'
for i in s:
	print (" ".join([key for key, value in dic.items() if value == i]),end='')

m = hashlib.md5()

m.update(*b*'this_is_flag')

print("flag{" + m.hexdigest() + "}")

easy_CRC · 92

题目

1:C4E68E3A
2:08FF301C
3:F6FBA587
4:B85C2F9A
5:F1B73D20
6:C6F1D9D7

flag=1+2+3+4+5+6
Each serial number consists of 4 characters

题解

已知明文长度的CRC爆破，具体学习可见：Python·CRC爆破学习

代码

import binascii
import string

# 四字节爆破
def crack_crc():
    print('-------------Start Crack CRC-------------')
    crc_list = [0xC4E68E3A, 0x08FF301C, 0xF6FBA587, 0xB85C2F9A, 0xF1B73D20, 0xC6F1D9D7]  # 文件的CRC32值列表，注意顺序
    comment = ''
    chars = string.printable
    for crc_value in crc_list:
        for char1 in chars:
            for char2 in chars:
                for char3 in chars:
                    for char4 in chars:
                        res_char = char1 + char2 + char3 + char4#获取遍历的任意4Byte字符
                        char_crc = binascii.crc32(res_char.encode())#获取遍历字符的CRC32值
                        calc_crc = char_crc & 0xffffffff#将遍历的字符的CRC32值与0xffffffff进行与运算
                        if calc_crc == crc_value:#将获取字符的CRC32值与每个文件的CRC32值进行匹配
                            print('[+] {}: {}'.format(hex(crc_value),res_char))
                            comment += res_char
    print('-----------CRC Crack Completed-----------')
    print('Result: {}'.format(comment))

if __name__ == '__main__':
    crack_crc()
    """
    -------------Start Crack CRC-------------
[+] 0xc4e68e3a: b323
[+] 0x8ff301c: 1e94
[+] 0xf6fba587: f045
[+] 0xb85c2f9a: e76e
[+] 0xf1b73d20: 5932
[+] 0xc6f1d9d7: 66f4
-----------CRC Crack Completed-----------
Result: b3231e94f045e76e593266f4
    """

Crypto_xor · 95

2018 AFCTF MagicNum · 86

题目

72065910510177138000000000000000.000000
71863209670811371000000.000000
18489682625412760000000000000000.000000
72723257588050687000000.000000
4674659167469766200000000.000000
19061698837499292000000000000000000000.000000

看不明白！

题解

流加密，待续

1837 · 86

题目

MTEgMTExIDAwMCAwMCAwMTExMSAwMDAgMDAxMCAwMDEgMTA

题解

1. base64解码

   11 111 000 00 01111 000 0010 001 10

   这里觉得好熟悉，卡了一会儿，在想1837

2. 摩斯电码解码

   flag{MOSI1SFUN}

总结

• 01码与摩斯电码的配合
• 1837年摩斯电码诞生

目前

主要在看RSA与BMZCTF刷题。

排名： 52 / 1605

答题情况

🧻❤️㊙️🐎